Linear Algebra for Data Science

To some extent, machine learning is simply multivariate statistics focused on prediction; and statistics, especially multivariate statistics, is, in a sense, an advanced application of linear algebra. This illustrates the importance of linear algebra as a mathematical tool. It not only plays a key role in computation but is also crucial for a deep understanding of algorithms.

So, how can you tell if your knowledge of linear algebra is sufficient? Take a look at the diagram below. If you can understand the logical relationships between the modules, then you’re good to go. If not, you may need to spend a bit more time reviewing.

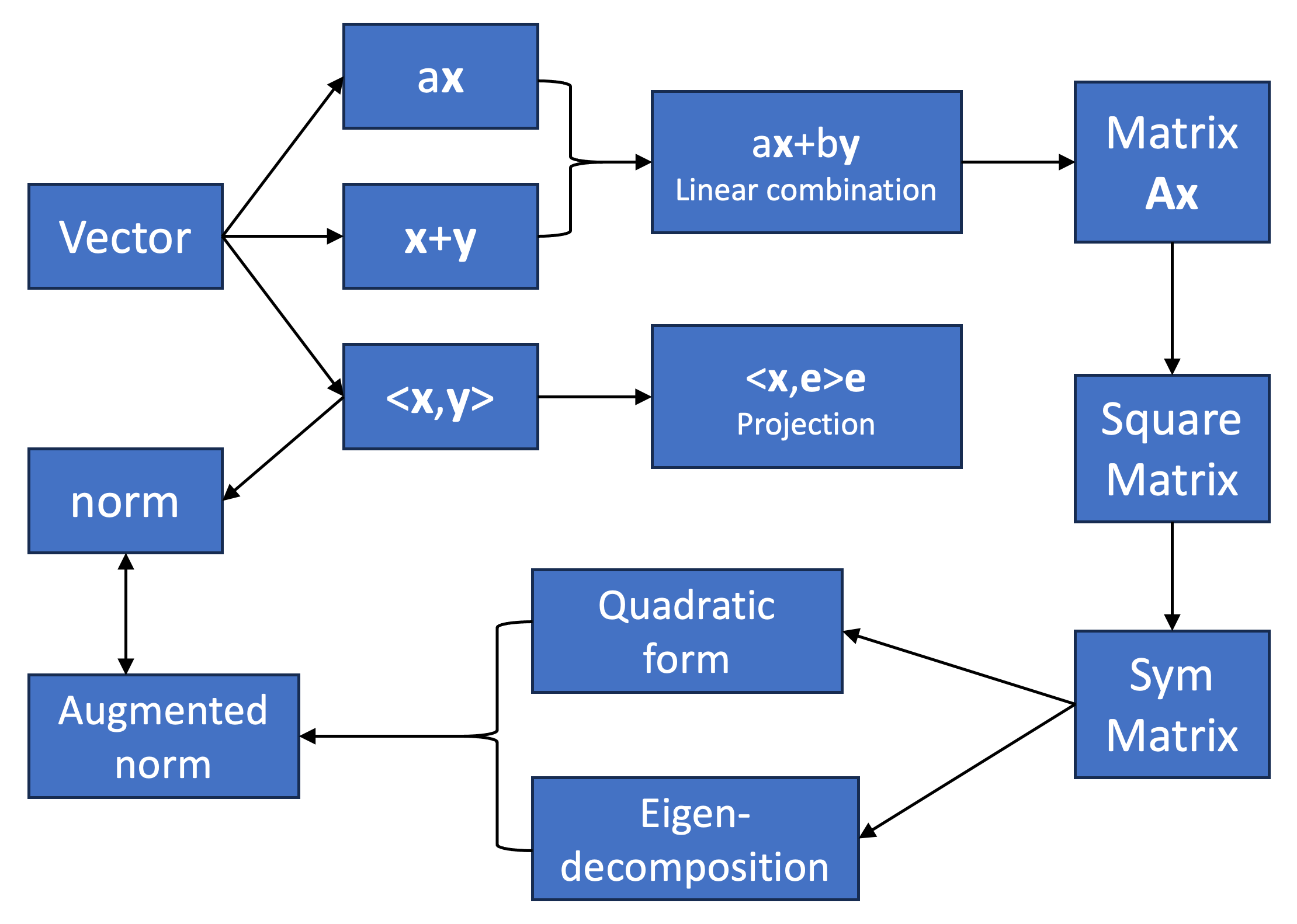
Linear algebra isn’t very beginner-friendly for many people. If you start with calculating determinants, finding inverse matrices, or computing eigenvalues and eigenvectors, you will likely be overwhelmed by its tedious calculations and the vast number of concepts to memorize. Even if you manage to get through it with sheer mental effort, the knowledge you acquire will be lifeless—it won’t serve you well, let alone blossom into something new.

So, what is the key to learning linear algebra? It’s understanding the geometric meaning. The idea of combining numbers and shapes can offer you a tangible lifeline in the depths of abstract concepts. There are plenty of helpful tutorials on linear algebra online, and among them, Professor Strang’s MIT OpenCourseWare is a must. Everyone should listen to his lectures at least once. In the era of social media, there’s no shortage of interesting creators explaining linear algebra with vivid animations, like 3Blue1Brown. Here, I provide a concise summary of linear algebra knowledge tailored for data science. The logic behind my summary follows the mind map above. I hope it helps you.