Vector
Array View:
What is a vector? First, a vector is an array of numbers. For example,
\[ \textbf{x} = \left( 38, 1, 170, 67, 2, 0 \right). \]
Conventionally, we use a lowercase letter in bold to denote a vector. There are two ways to arrange these numbers, horizontally or vertically. If we stack the numbers vertically, then I get a column vector, like this
\[ \textbf{x} = \begin{pmatrix} 38\\ 1\\ 170\\ 67\\ 2\\ 0 \end{pmatrix} \] Conventionally, again, it defaults to a column vector when we say a vector. However, a column vector takes much space, therefore people place it flat as a row vector and add a little “T” in the upper right corner.
\[ \textbf{x} = \left( 38, 1, 170, 67, 2, 0 \right)^{\top}. \]
The little “T” denotes an operation, transpose, which means changing the size of the array from (1,7) to (7,1). Thus vector is still a column vector.
In data science, there usually are two ways to understand a vector. First, it can be viewed as a single case with observations on several variables. We call this vector as an observation, or a case, or an example. For example, the vector above presents a 38 year old guy’s (1 indicates male) basic information. Hight is 170, weight is 67, he has two kids, and the number of pub visits per month is 0. He is probably a home guy.
Another example is displayed in the following 3D scatter plot. You can move your cursor to a certain point, and you’ll find a string of numbers. Each string of numbers represents a flower, and all the flowers are blooming in this 3D world, which we usually call the feature space.
Second, it also can be understood as a sample of a single variable. For example, \[ (1.78, 1.85, 1.74, 1.82, 1.90, 1.88)^{\top} \] it is a sample of height of audlt Swedish men.
Geometry View
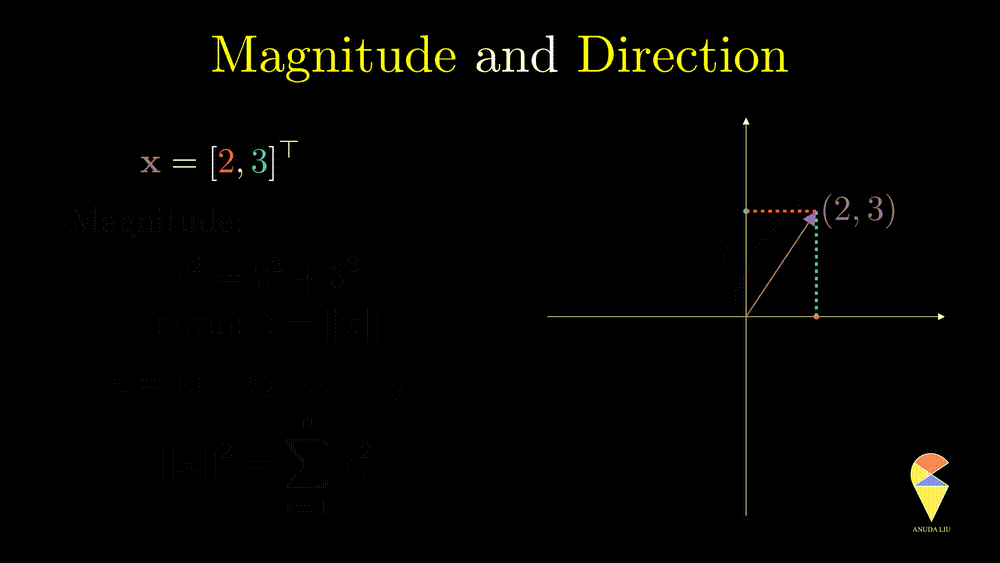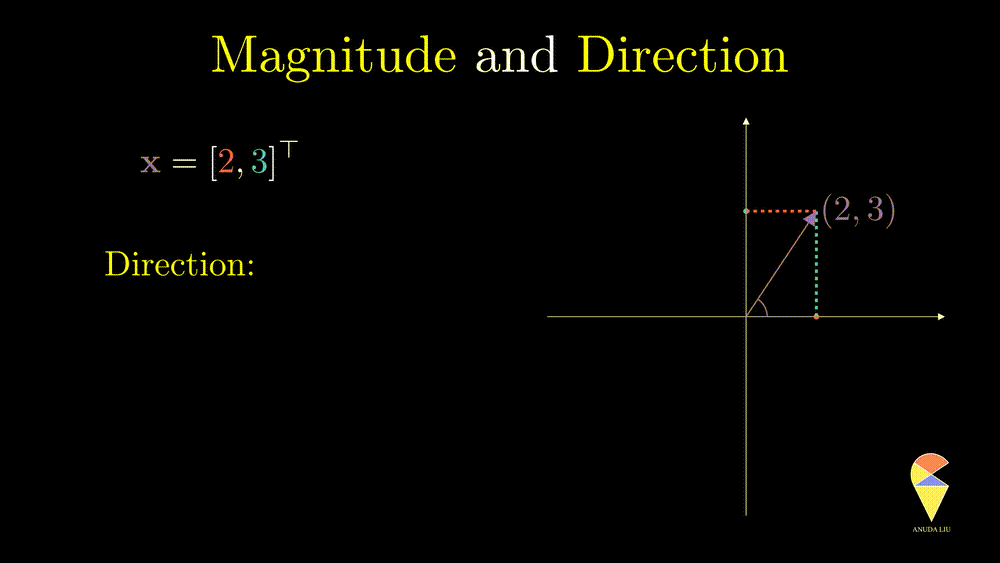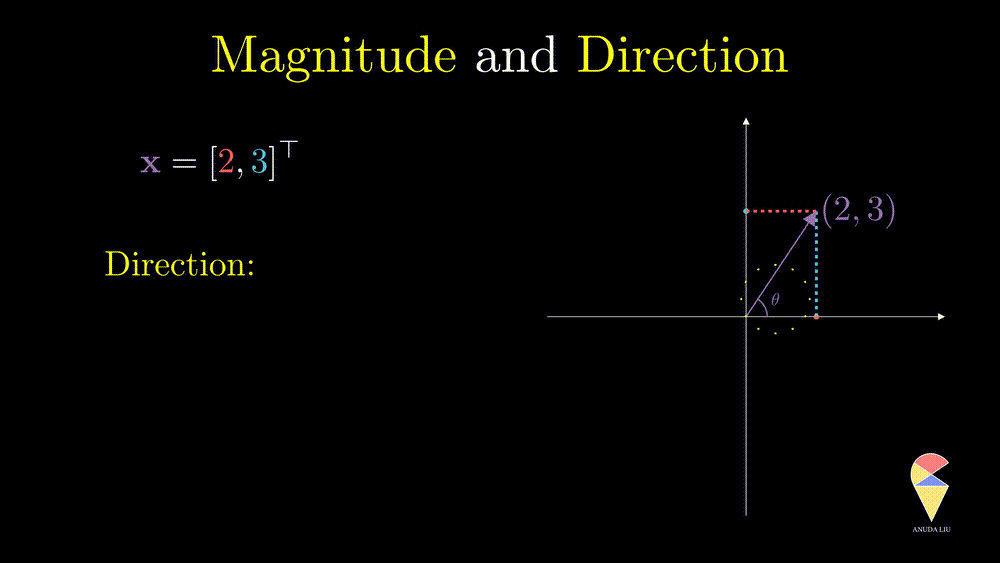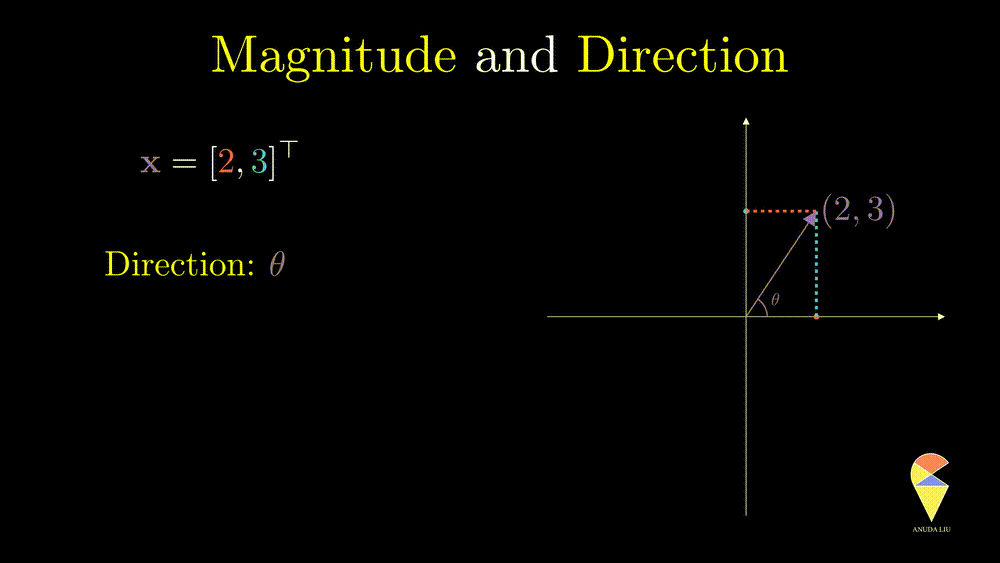
Another understanding is to understand a vector from a geometric point of view as a directed line segment starting from the origin in the coordinate space and ending at the point of this string of numbers in the space. Here is an example of a vector in a 2D space.

This way of understanding allows us to learn linear algebra intuitively from a geometric point of view. For example, we can quantify a vector from two geometric perspectives, i.e. magnitude and direction. The magnitude of a vector can be quantified by the length of the corresponding arrow and we call it as norm. For a general vector \(\textbf{x} = \left( x_1, x_2, \dots, x_n \right)^{\top}\), its norm is \(\|\textbf{x}\|=\sqrt{ \sum_{i=1}^n x^2_i }\).

Direction is another important characteristic of a vector. The angle between the vector and x-axes can determine it. How can the angle be quantified? We will return to it when discussing an important operator in linear algebra, the inner product.
Let’s go ahead and study more from a geometric point of view.
