Linear Combination
Inspired by subtraction, it is obvious that if one changes the coefficients, then we will end up with another vector.
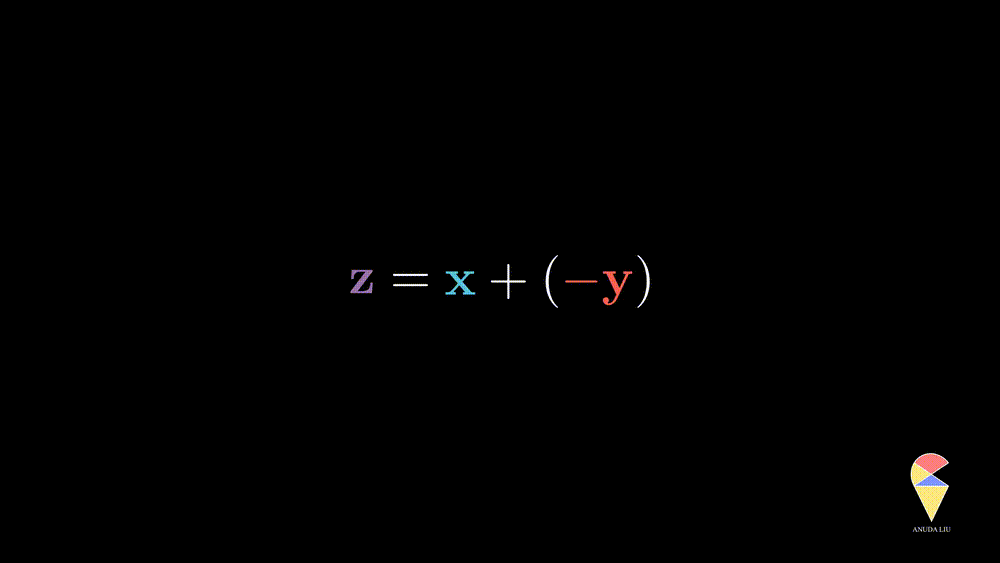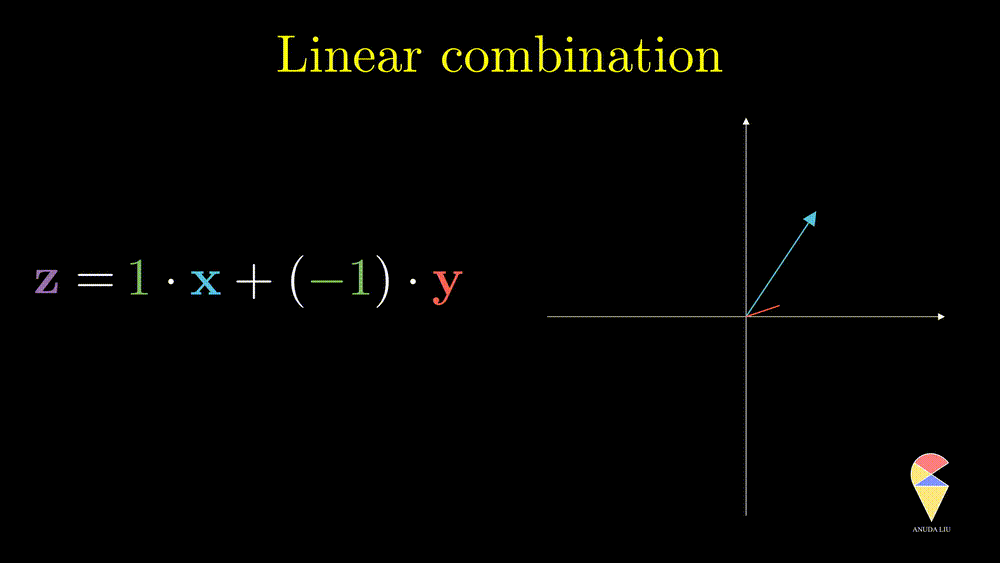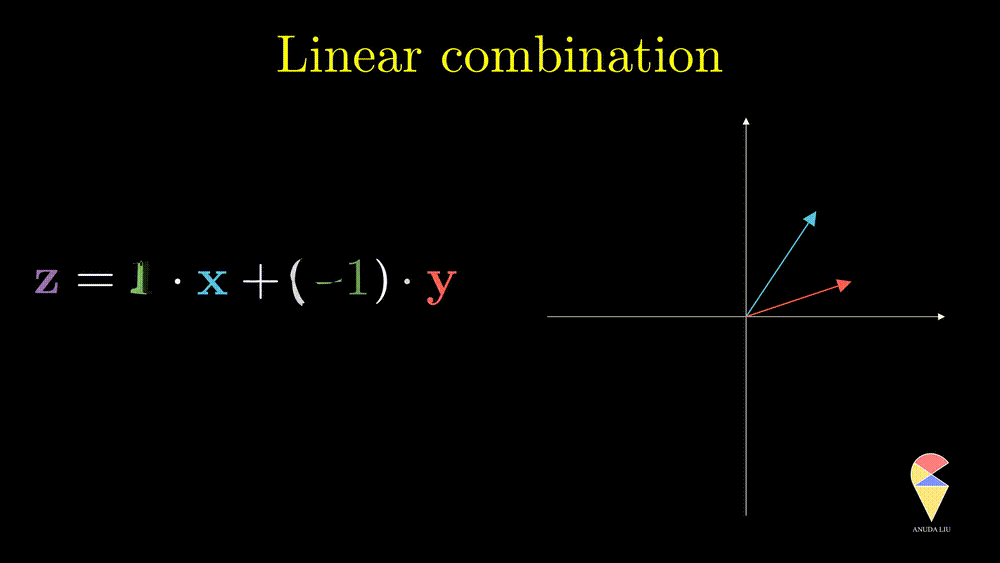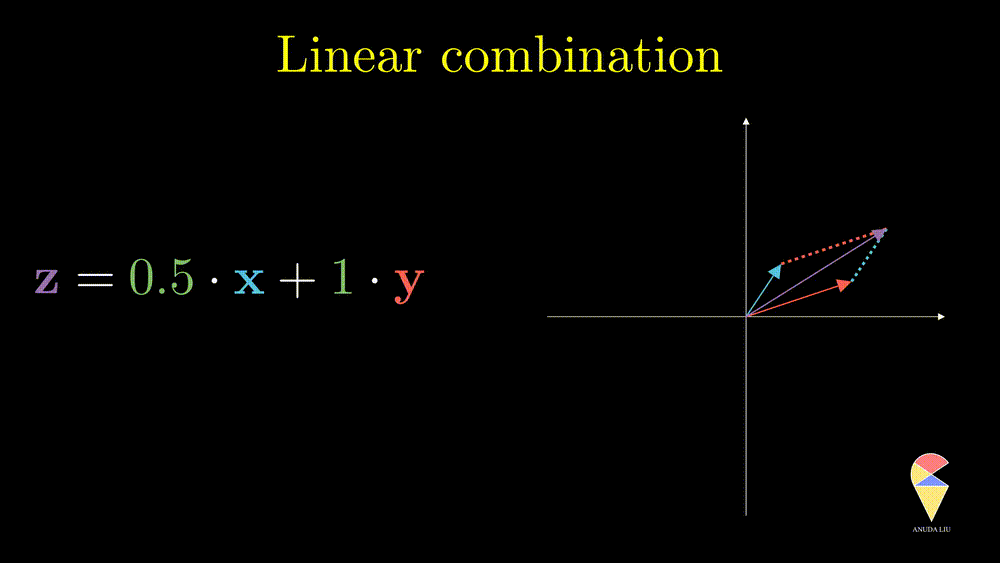
Inversely, we also can find two proper coefficients such that an arbitrary vector (purple) can be represented as the sum of two given vectors (red and blue).
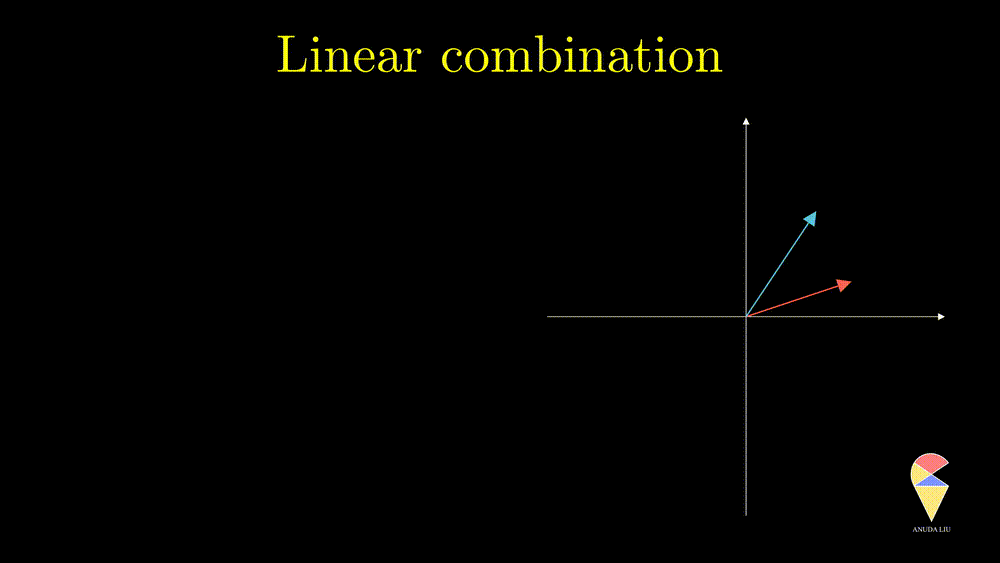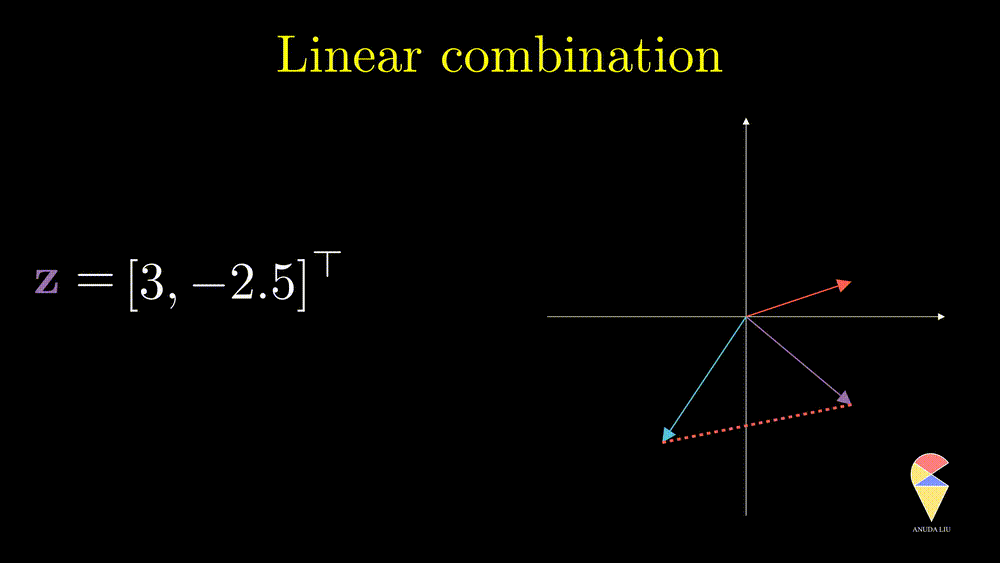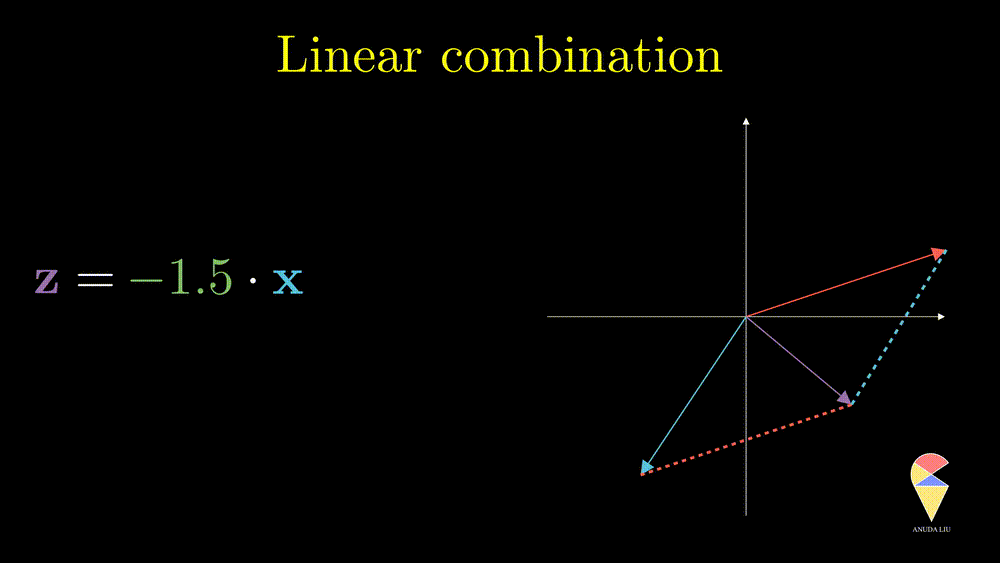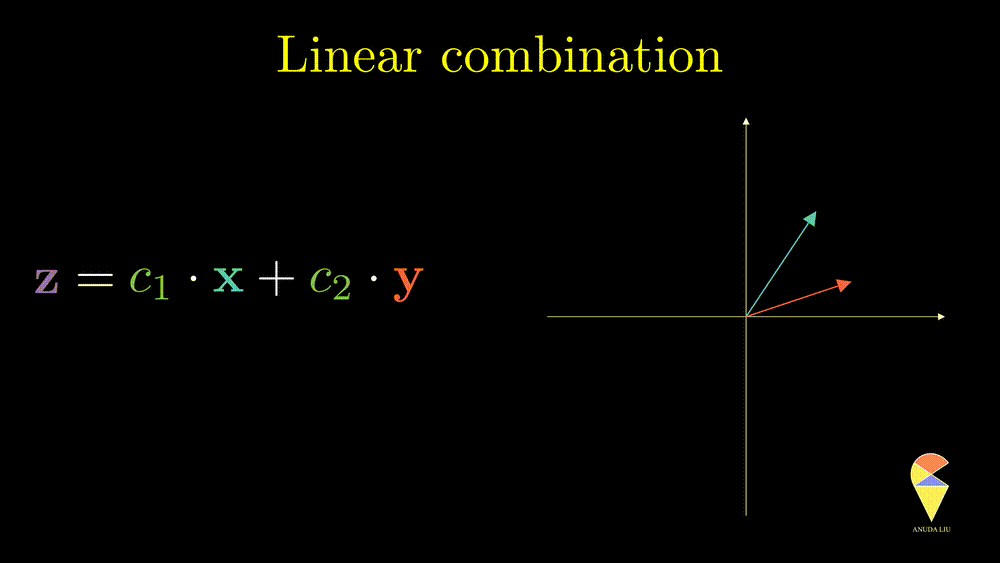
So, the linear combination of two vectors is \(c_1\textbf{x}_1 + c_2\textbf{x}_2.\) In general, the linear combination can be defined as the weighted sum of a group of vectors. For \(\textbf{x}_1, \textbf{x}_2, \dots, \textbf{x}_n\), and n scalars \(c_1, c_2, \dots, c_n\), the linear combination is presented as \(\sum_{i=1}^n c_i\textbf{x}_i\).
It seems that we can create all the vectors as long as hold two vectors in a 2D space. However, that is not always true.
