Linear Independent
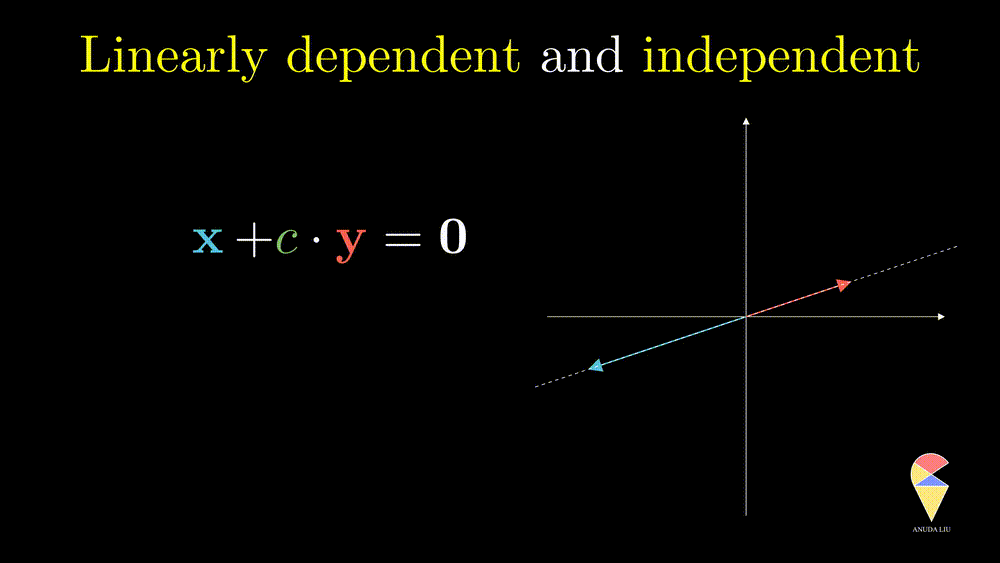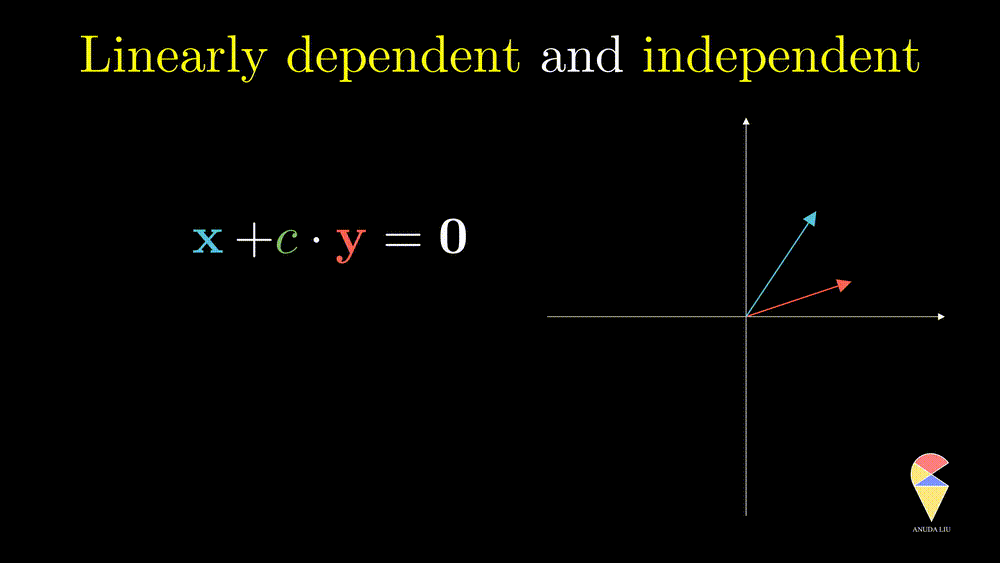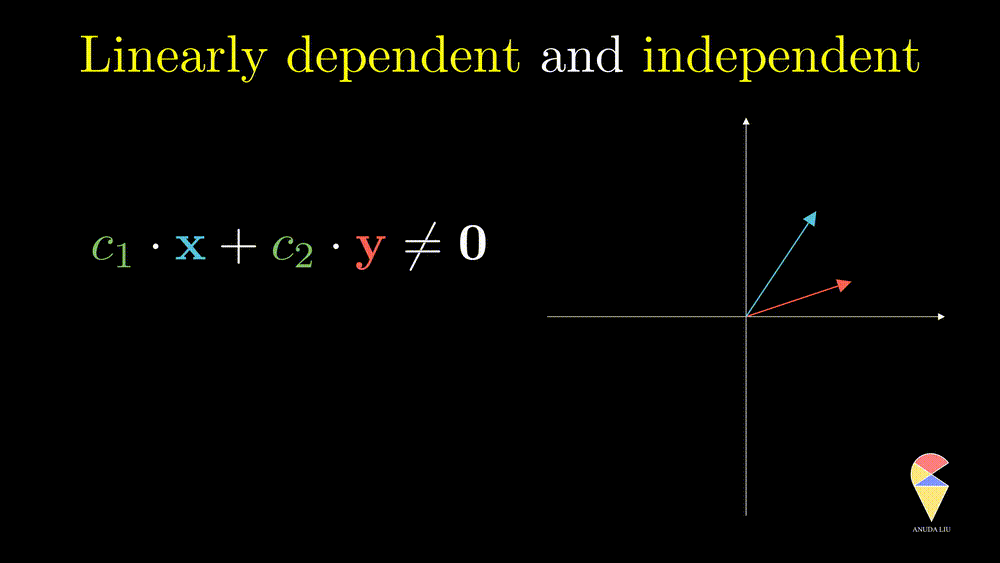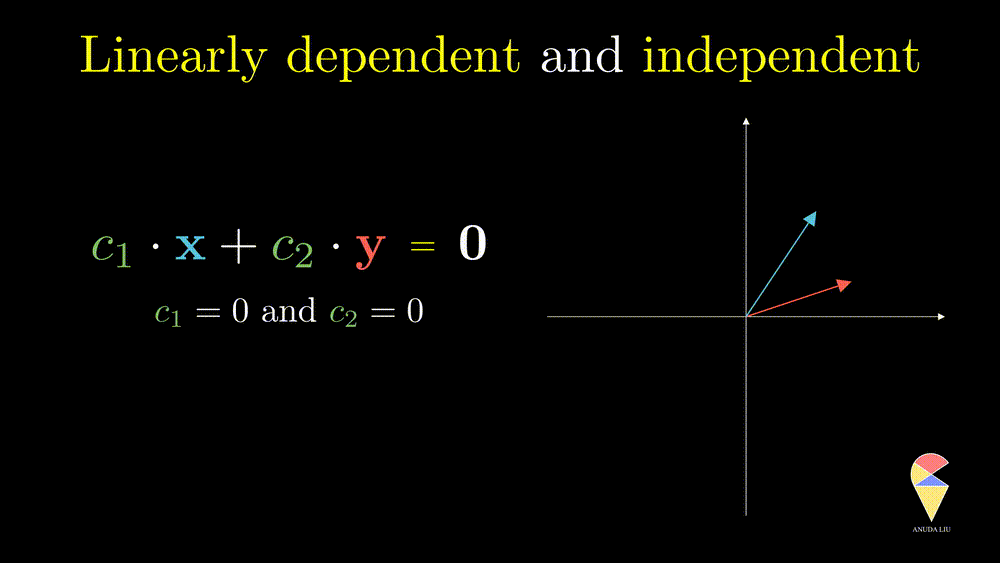
Next, I will show you one simple counter-example. Considering two vectors pointing in the same direction, we know that one vector can be represented as another vector scaled by some scalar. Therefore, the linear combination of the two vectors is equivalent to a scalar multiplication of arbitrary one vector. In this case, the resulting vector only stays in one direction or presents a line but not the 2D plane. Thus, we can’t create arbitrary vectors by the two vectors through linear combinations. It is also the case when the two vectors point in opposite directions.
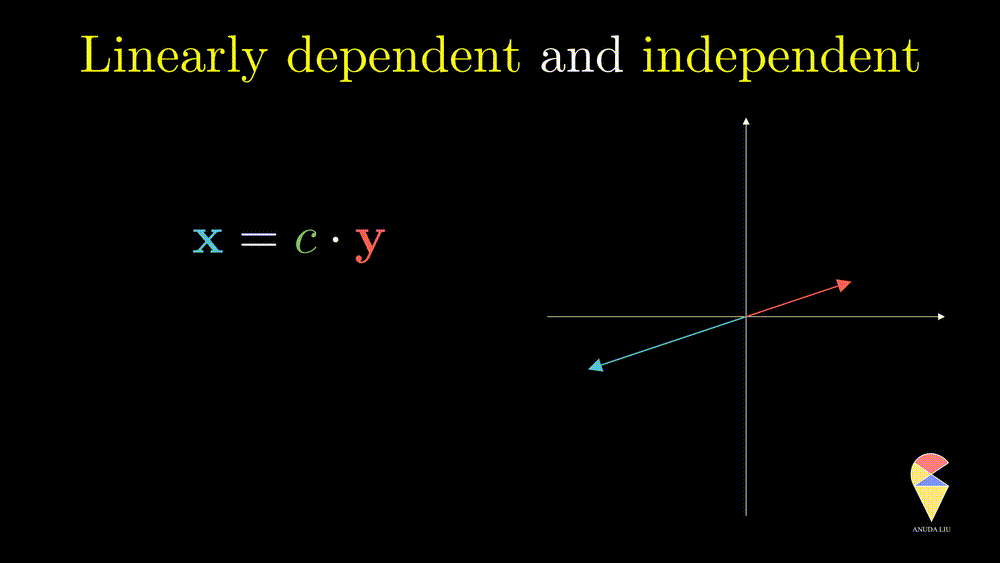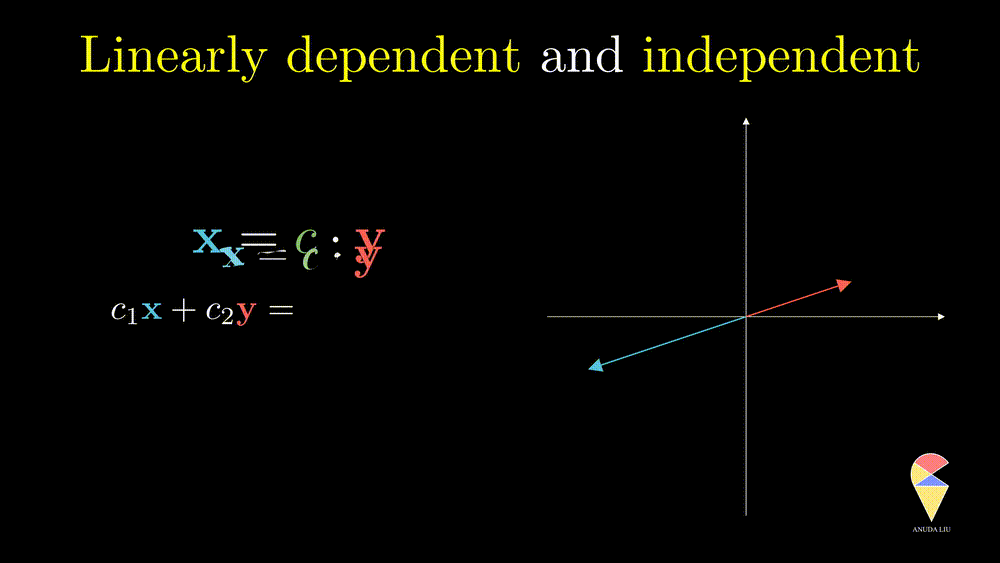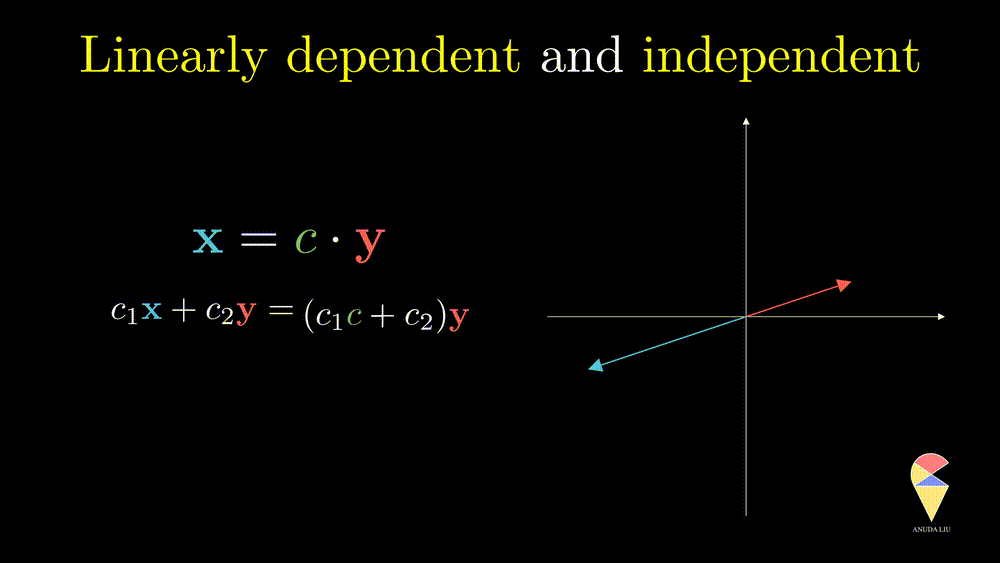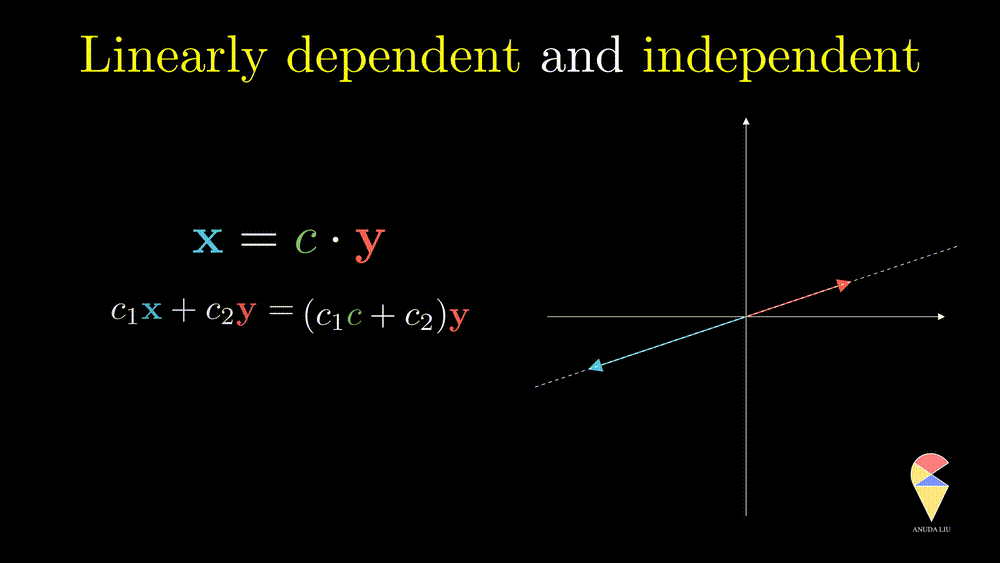
In simple words, for two overlapping vectors, we can only create a new vector in the direction of two vectors. In a mathematical language, we can use a linear combination of two vectors with non-zero coefficients to get the zero vector. In this case, we say the two vectors are linearly dependent.
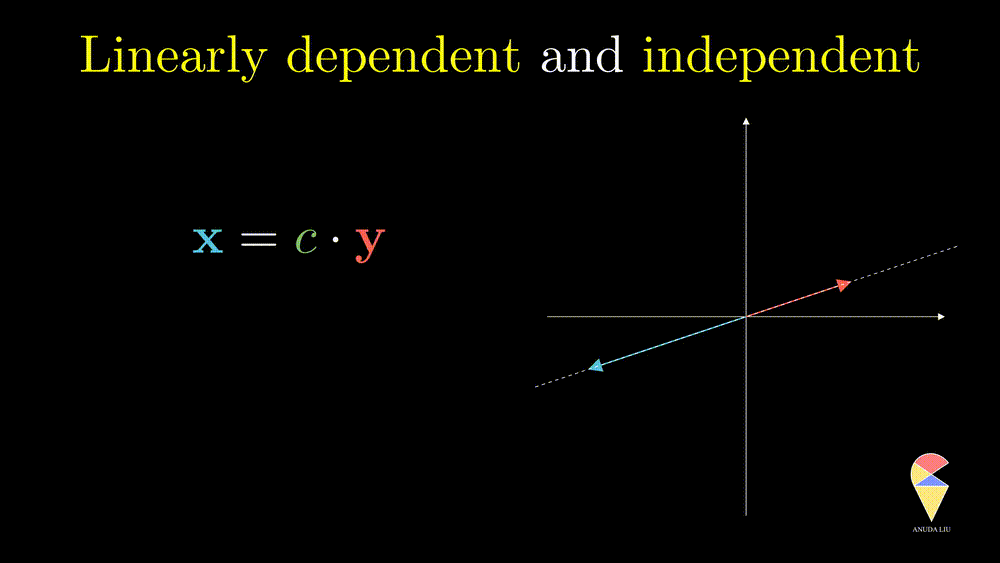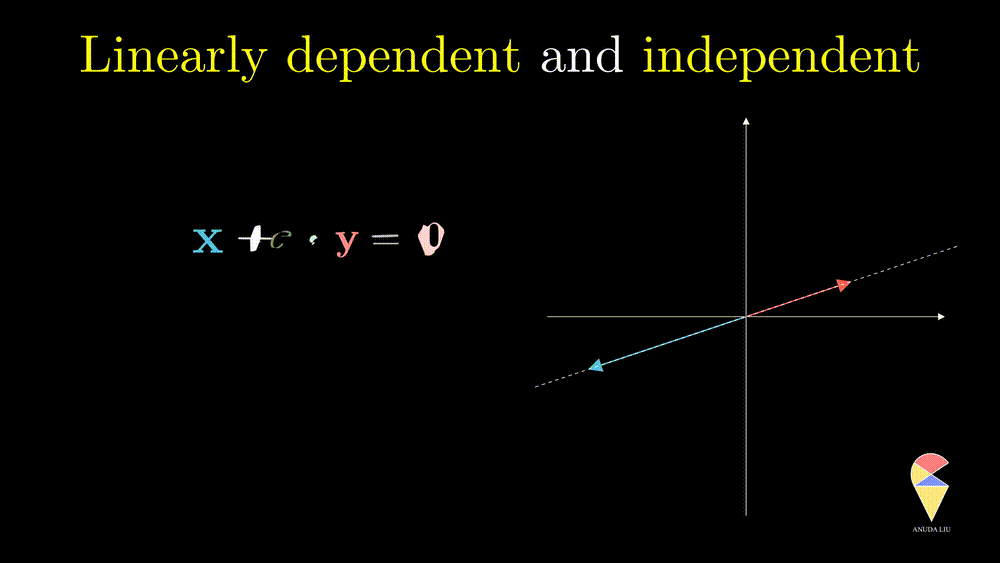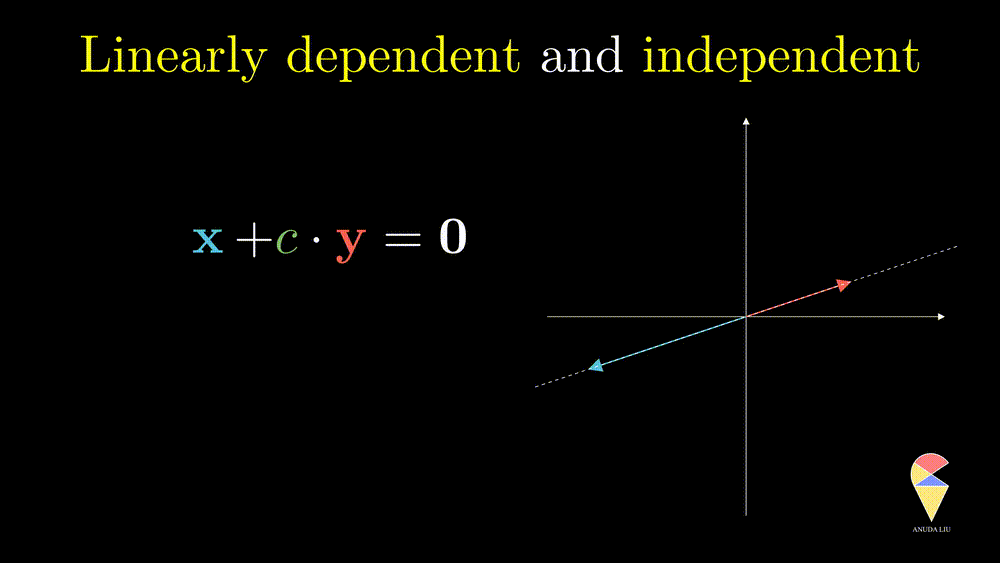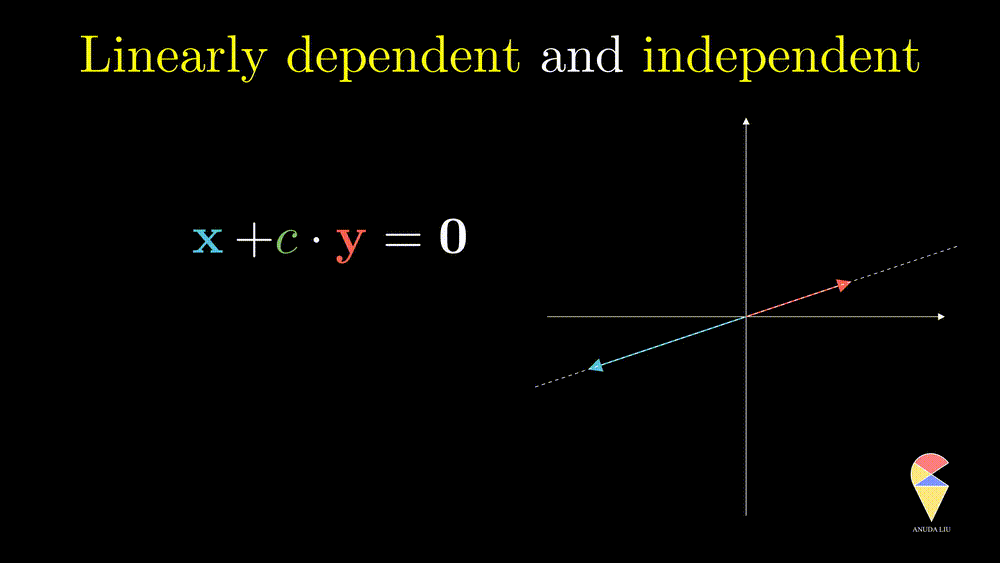
Oppositely, for two non-overlapping vectors, we can’t use a linear combination of them to create the zero vector unless the coefficients all are zeros, and we say the two vectors are linearly independent.
This definition can be extended to a more general scenario and leads to the general definition of linear dependence.

- For 2D space, we can maximumly have two linearly independent vectors. For k-D space, we can maximumly have k linearly independent vectors. Is that true?
Great! It is a good time to introduce the next concept, basis, which is not only important in linear algebra but also in data analysis.
