Inner Product
So far, we have defined one operation on two vectors, i.e. addition, and can see the power of geometry. In order to use more intuitive geometric ideas, we need to introduce another operation on two vectors, that is the inner product.
Inner product, at first sight
The inner product is also well known as the dot product. Here we use the inner product notations. For two vectors \(\textbf{x} = \left( x_1, x_2, \dots, x_n\right)^{\top}\) and \(\textbf{y} = \left( y_1, y_2, \dots, y_n\right)^{\top},\) the inner product is \(\langle \textbf{x}, \textbf{y} \rangle = \textbf{x}^{\top}\textbf{y} = \sum_{i=1}^n x_iy_i\). In textbooks in certain disciplines, the inner product is also represented as \(\textbf{x} \cdot \textbf{y}\).

Remark 1: Since the inner product of two vectors is a scalar, the result doesn’t depend on the order of two vectors.
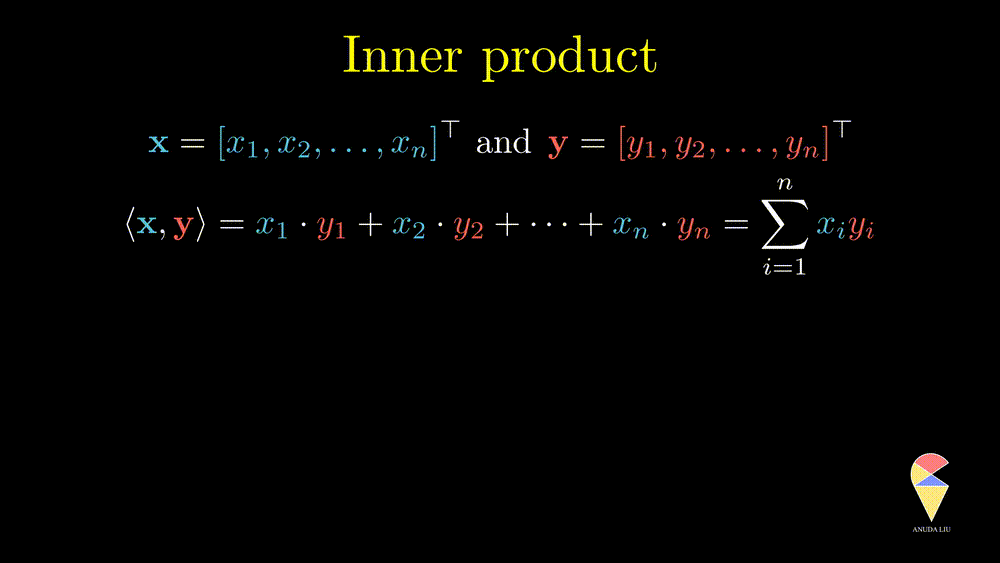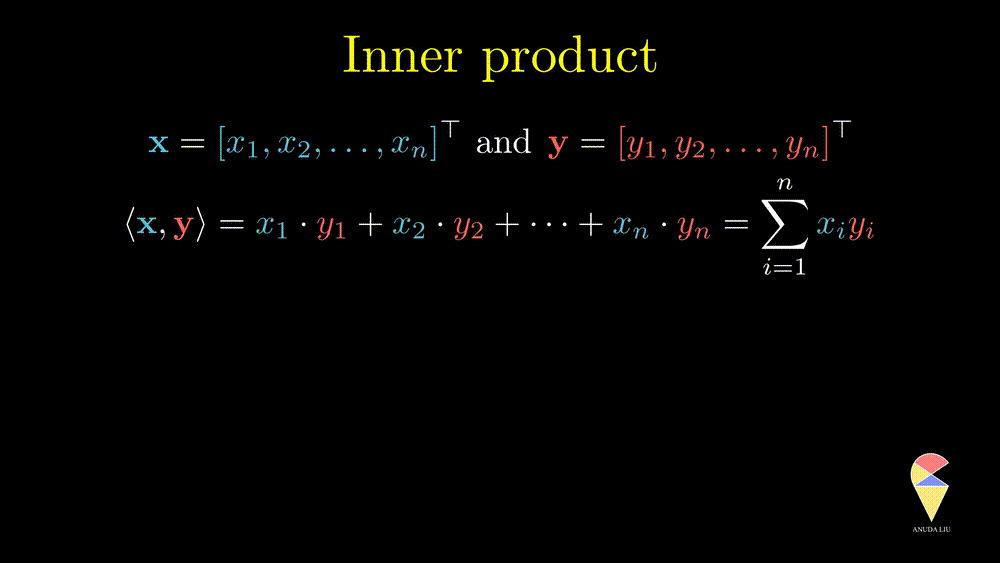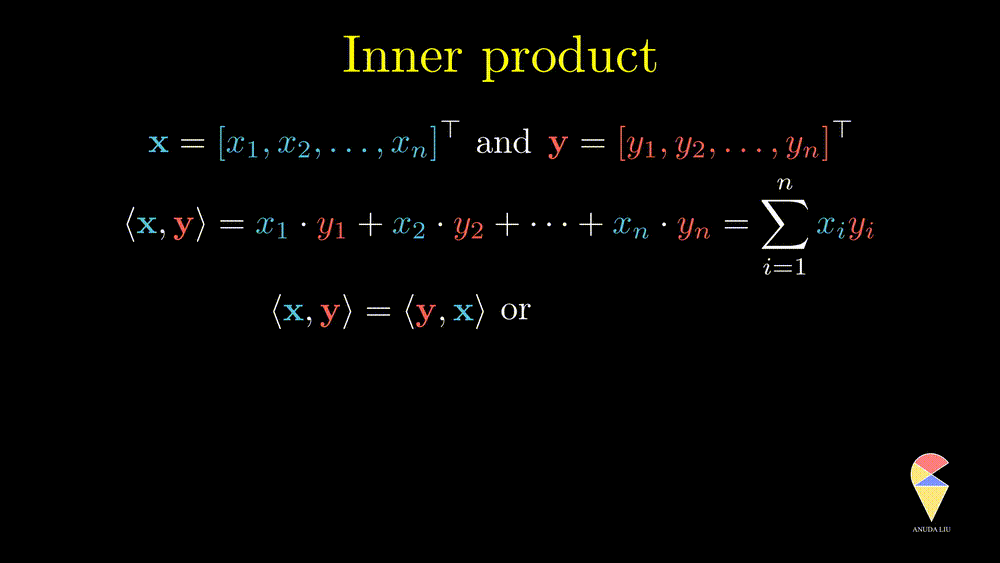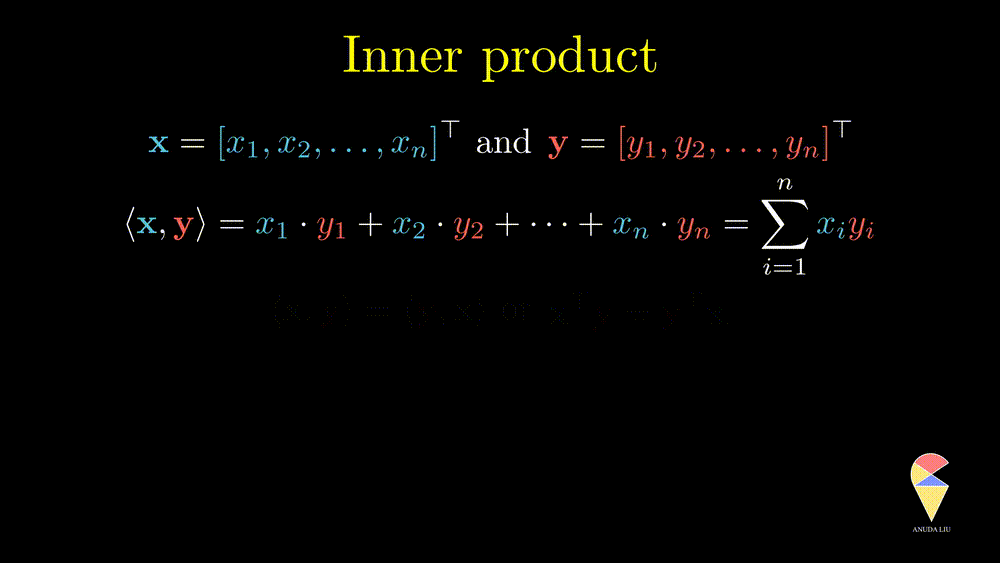
Remark 2: A special case is the inner product of a vector and itself. We actually have seen it before and it is the square of norm of this vector.
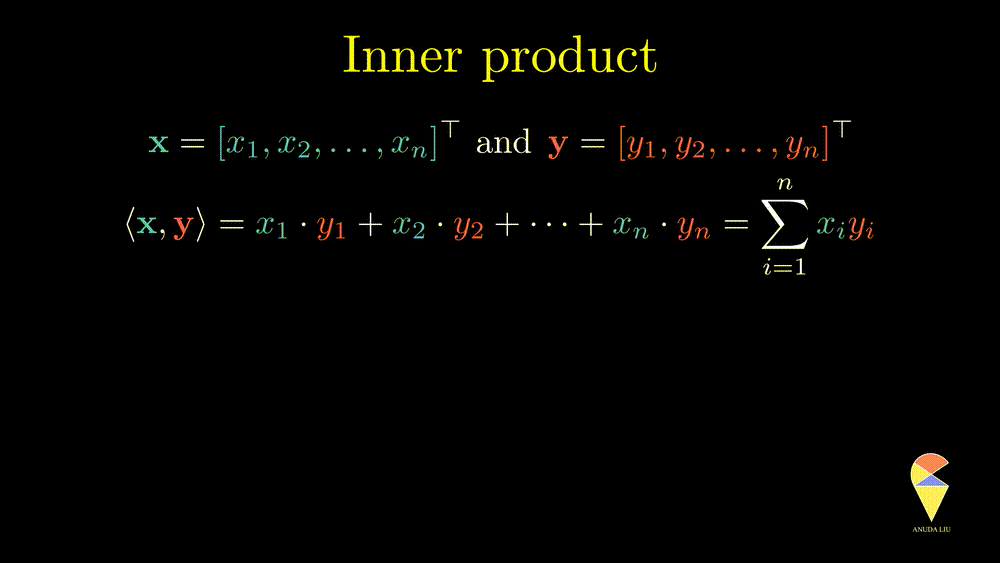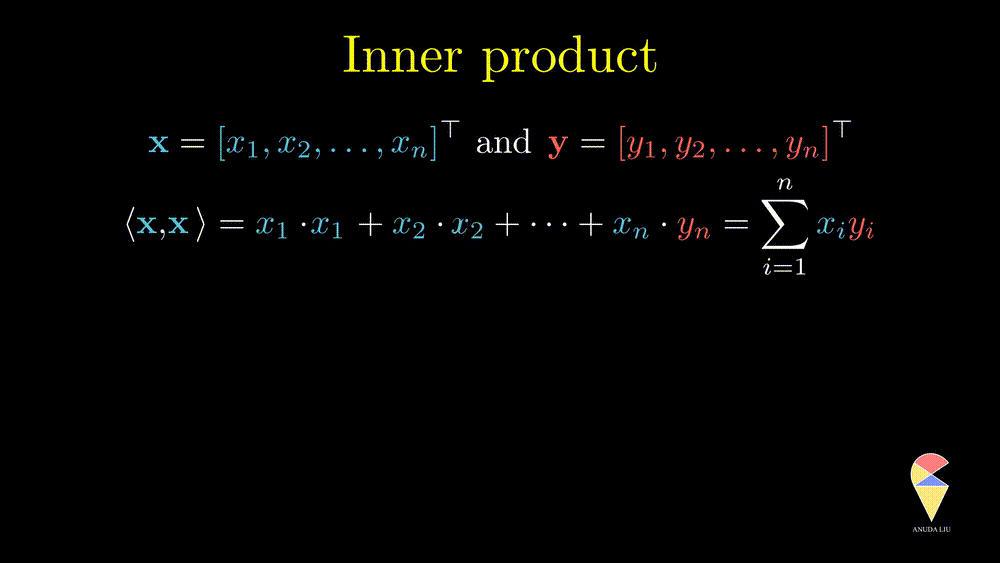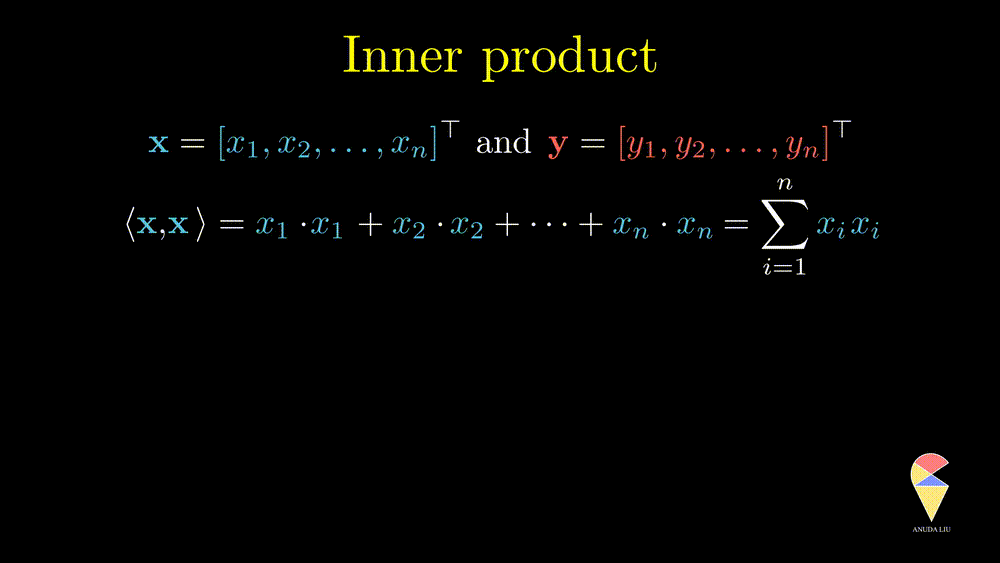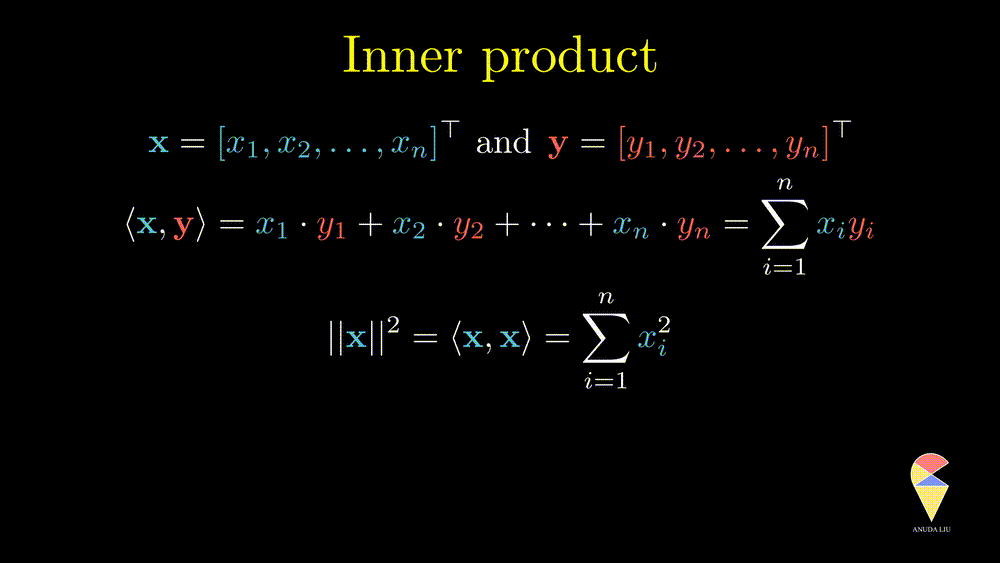
Inner product, the geometric view
In a 2D space, two non-overlapping vectors can form a triangle. Based on the cosine theorem, one can show that the inner product of two vectors is equal to the cosine value of the angle between two vectors times the product of the length of two vectors, i.e.
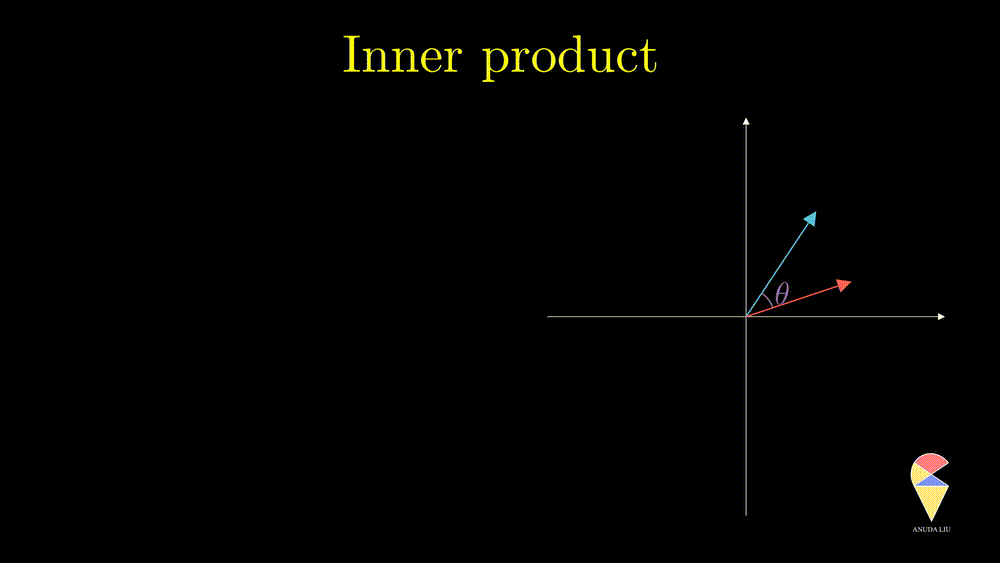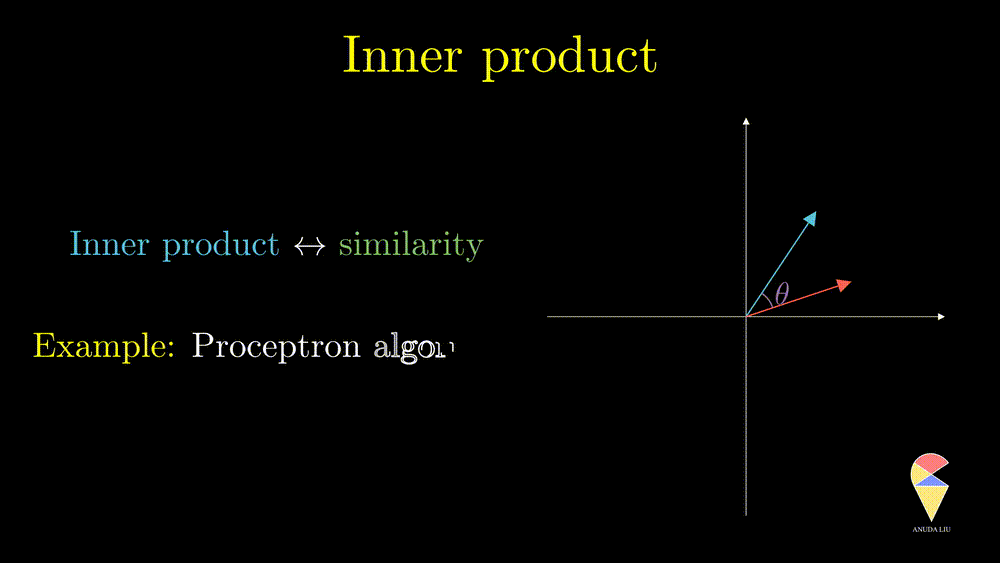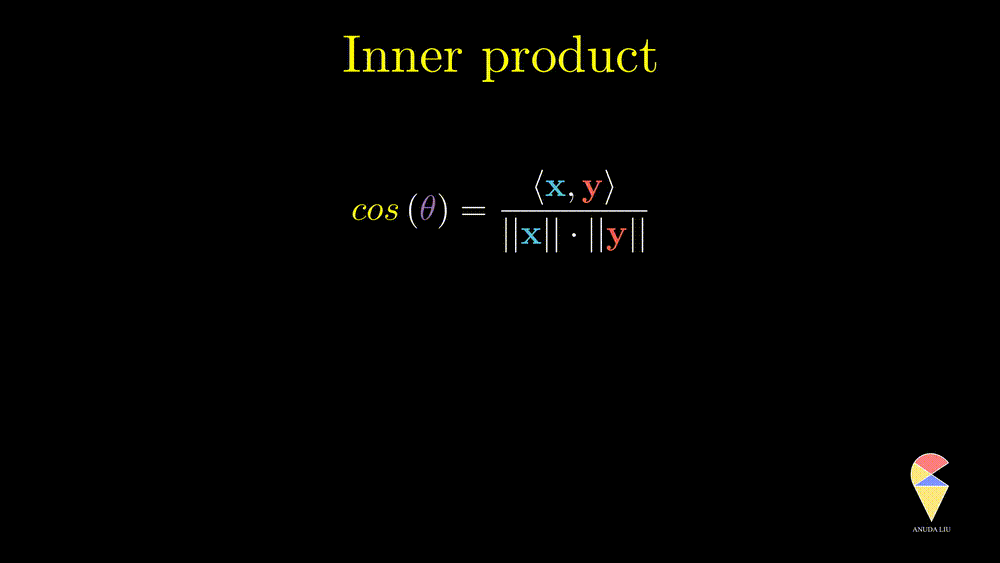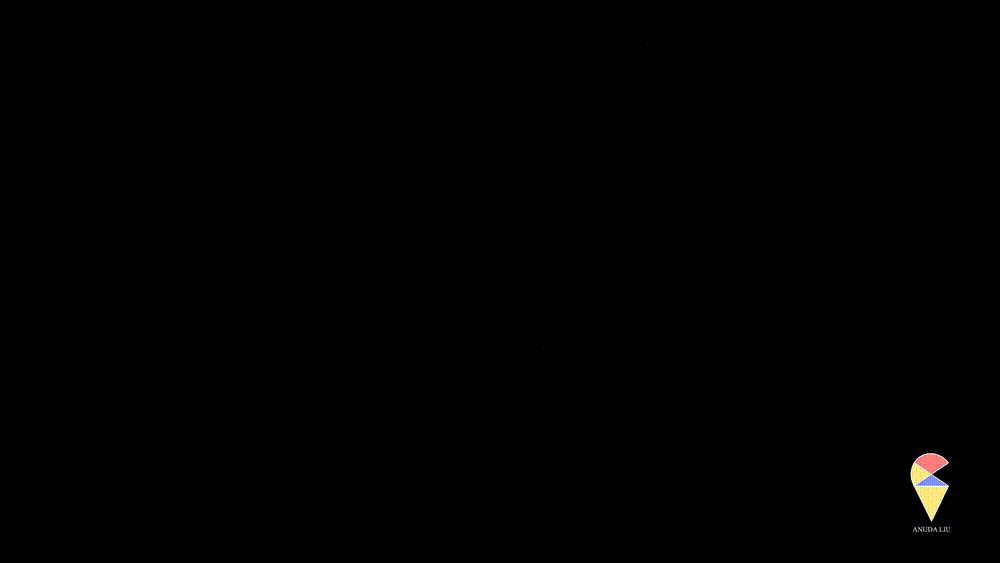
\[ \langle \textbf{x}, \textbf{y} \rangle = \textbf{x}^{\top}\textbf{y} = cos(\theta)\cdot ||\textbf{x} ||||\textbf{y}|| \]
If the two vectors all are unit vectors, then the inner product is equal to the cosine value of the angle between the two vectors. In one word, the inner product of two vectors is proportional to the cosine value of the angle between two vectors, i.e. \(\langle \textbf{x}, \textbf{y} \rangle = \textbf{x}^{\top}\textbf{y} \propto cos(\theta).\) Now, the connection between geometry and algebra has been established.

Based on this geometrical idea, one may have realized that the inner product quantifies the similarity of two vectors since the angle indicates if the two vectors are close to each other. This idea is very important in data science and it has been applied in a proptotpye algorithm in machine learning, that is the well-known algorithm, perceptron algorithm. In statistics, one famous statistic is just based on the inner product. Do you know what is that?
We have seen that there is a strong connection between inner product and the angle between two vectors. In our real life and mathematics, an angle of 90 degrees is special and the most useful one and it leads to the next concept, orthogonal.
