Orthogonal and Projection
Orthogonal
In linear algebra, if the angle between two vectors is 90 degrees, then we say they are orthogonal.
Recall your knowledge in high school, the cosine value of 90 degrees is 0. This fact provides a simple method to determine whether two vectors are orthogonal, i.e. two vectors are orthogonal if and only if their inner product is zero.
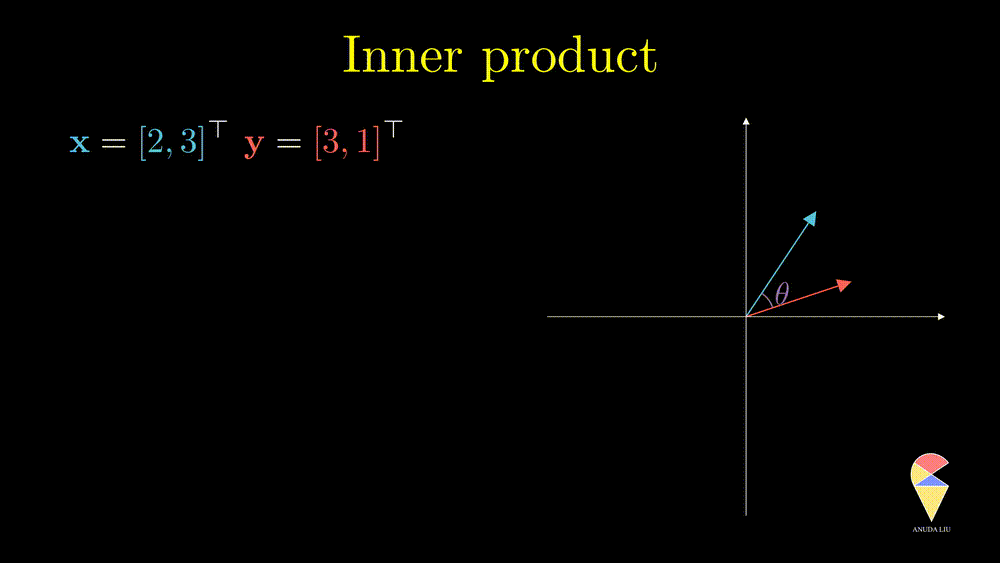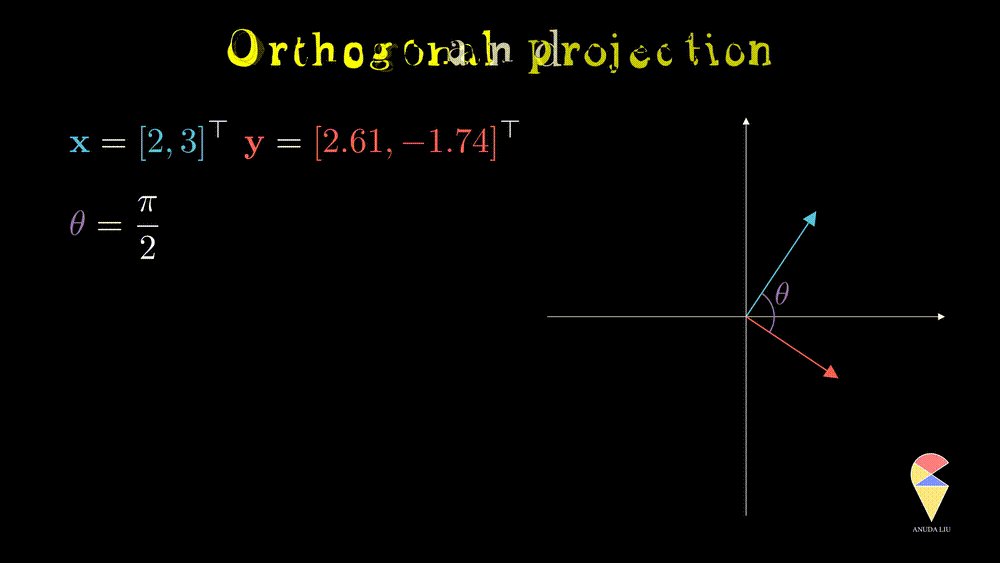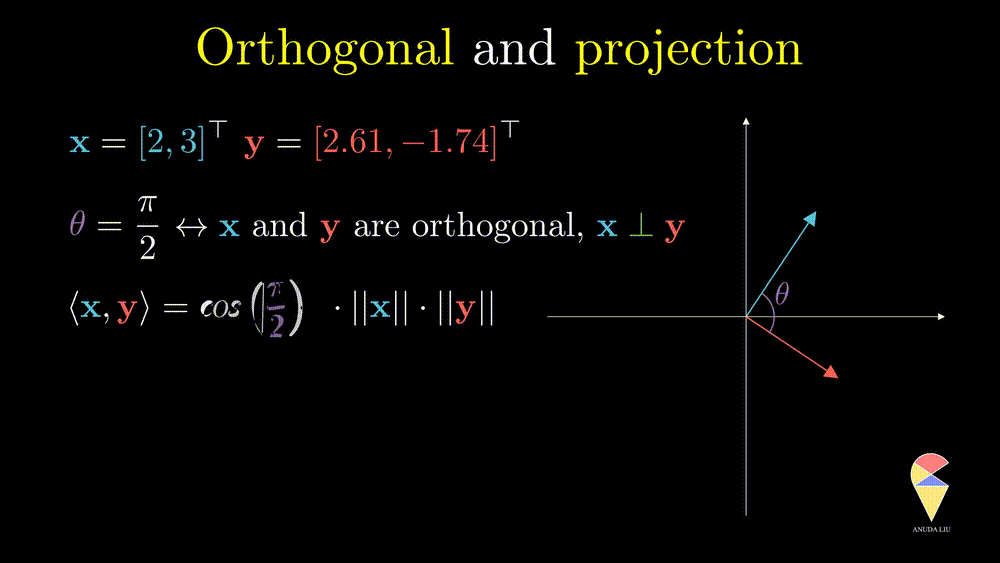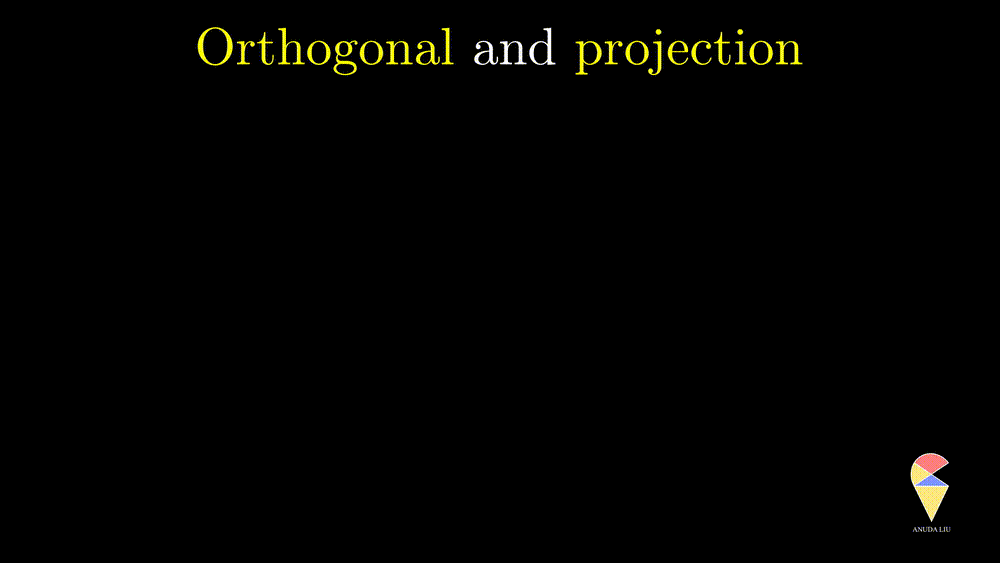
Orthogonal is an important concept in many ways. In statistics, there is a simple and good example. From the previous section, we learned that the correlation between two variables is just the cosine value of the angle between two variables. So if two variables are orthogonal, then they are also uncorrelated. Another reason is that the concept of orthogonal leads to the next important concept, projection.
Projection
A projection can be viewed as a vector created by two vectors through the following procedure. Suppose we have two non-overlapping vectors \(\textbf{x}\) and \(\textbf{y}\), a beam of light is incident from a direction perpendicular to \(\textbf{y}\) cause a shadow of \(\textbf{x}\) on \(\textbf{y}\) and the shadow is called the projection of \(\textbf{x}\) onto \(\textbf{y}\).
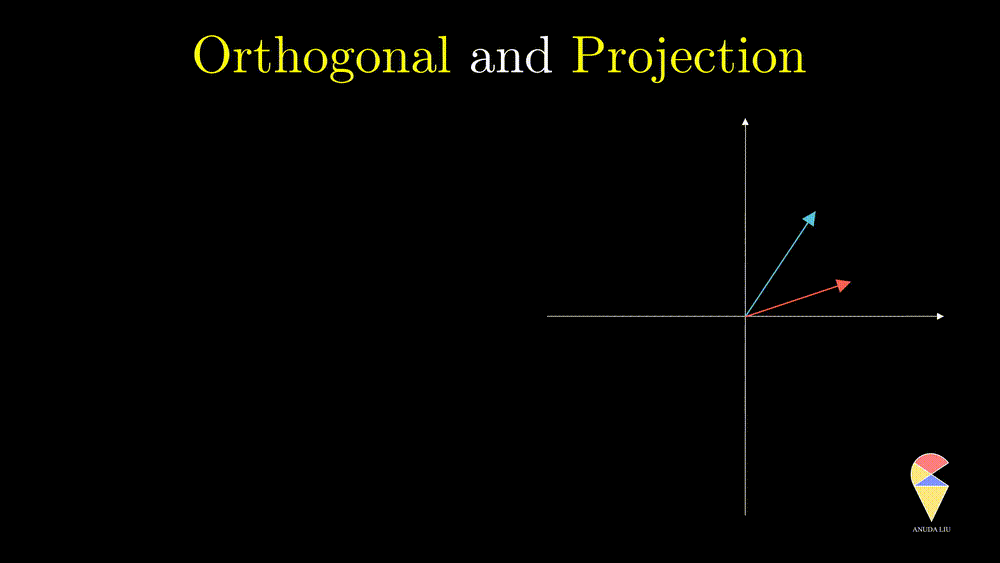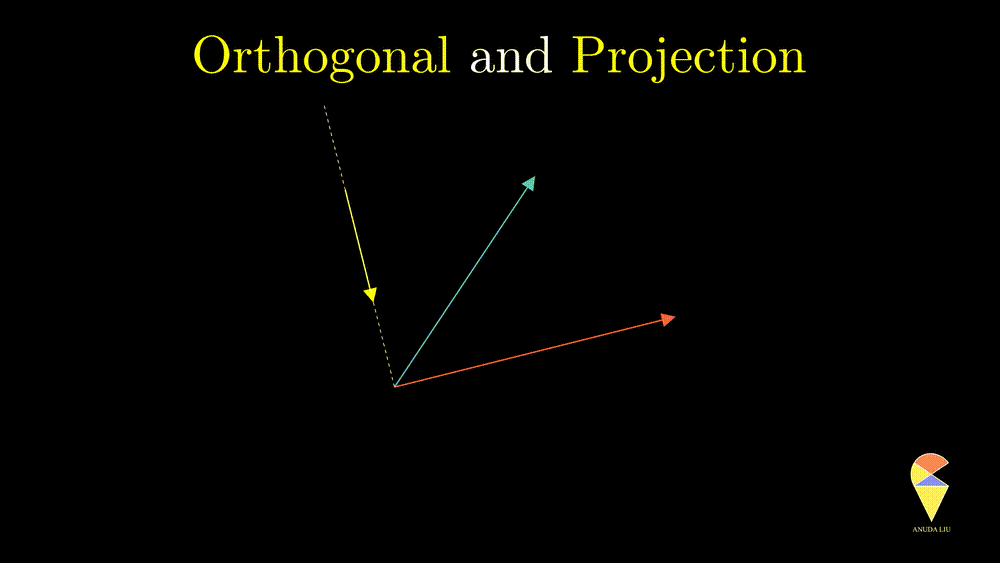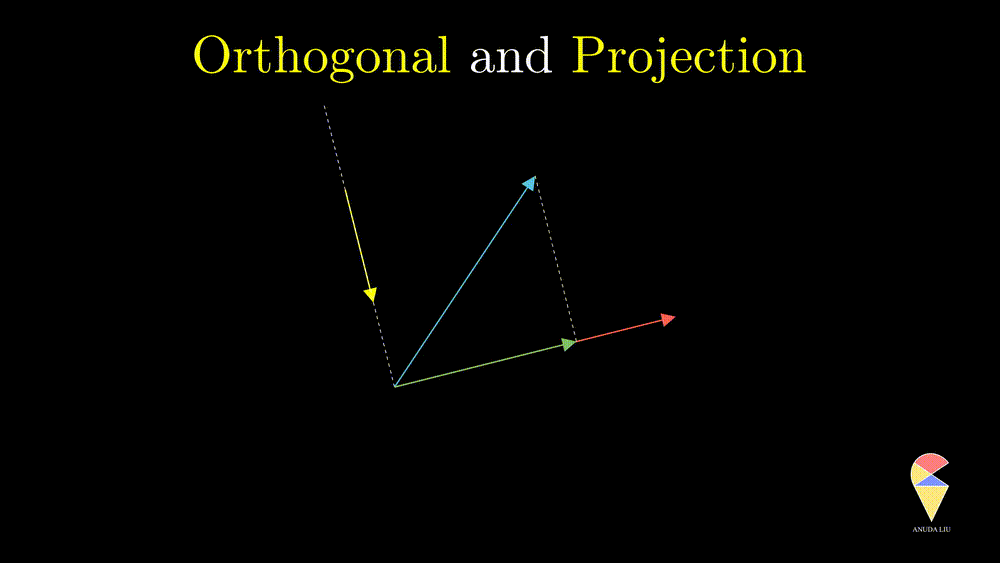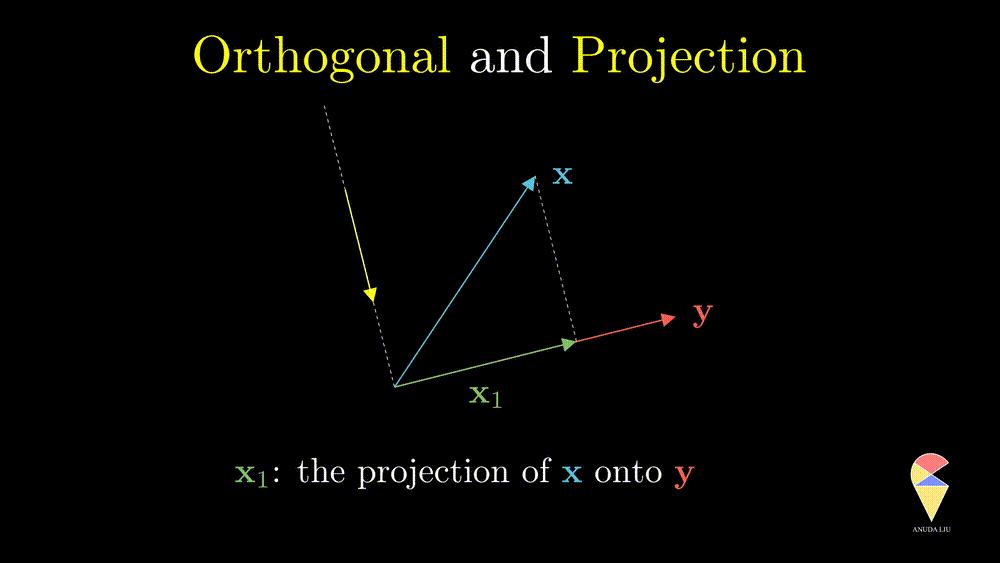
One interesting problem is how to represent the shadow \(\textbf{x}_1\) by the two existing vectors. You may have realized that \(\textbf{x}_1\) overlaps with vector \(\textbf{y}\), therefore \(\textbf{x}_1\) should be scaled \(\textbf{y}\), i.e. \(\textbf{x}_1 = k \cdot \textbf{y}\). So the problem becomes finding the coefficient \(k\). Based on the orthogonal properties, we can find that
\[ k = \frac{\textbf{x}^{\top} \textbf{y}}{\textbf{y}^{\top} \textbf{y}} \text{, and } \textbf{x}_1 = \frac{\textbf{x}^{\top} \textbf{y}}{\textbf{y}^{\top} \textbf{y}} \textbf{y}. \] through the following derivations.
Remark: The scalar \(k\) is just the length of projection and it is called scalar projection. One can go further and find that the scalar projection is obtained by the inner product of \(\textbf{x}\) and the unit vector in \(\textbf{y}\) direction.

Orthonormal Basis
In 2D space, there is a pair of two special and nice unit vectors, \((1,0)^{\top}\) and \((0,1)^{\top}\). One can easily get the scalar projection of arbitrary vectors on them, isn’t it? Obviously, they also form a basis of 2D space. This basis is very nice since they are not only unit vectors but also orthogonal to each other. We call this kind of basis an orthonormal basis.
