Matrix, its true color
At first sight
The most straightforward definition of a matrix is the rectangle array. One needs to use two numbers to describe the size (shape) of a matrix, the numbers of rows and columns. In the following example, the matrix consists of 3 rows and 4 columns. We say it is a 3 by 4 matrix. One neat but informative notation is \(\textbf{A} = \left\{ a_{ij} \right\}_{3 \times 4}\). In this course, keep in mind, we always use \(i\) indicates for the row index and \(j\) for column index.

You may remember the idea in the previous section that a matrix can be viewed as a “row vector” of column vectors. In this example, suppose we can find 3 linearly independent vectors from the 4 column vectors, then they can be viewed as a basis and generate a space. Similarly, the matrix also can be viewed as a “column vector” of row vectors, and they also can generate a space if they are linearly independent. In statistics, especially MDA, we mainly work with a data matrix. Let’s talk about it later on.
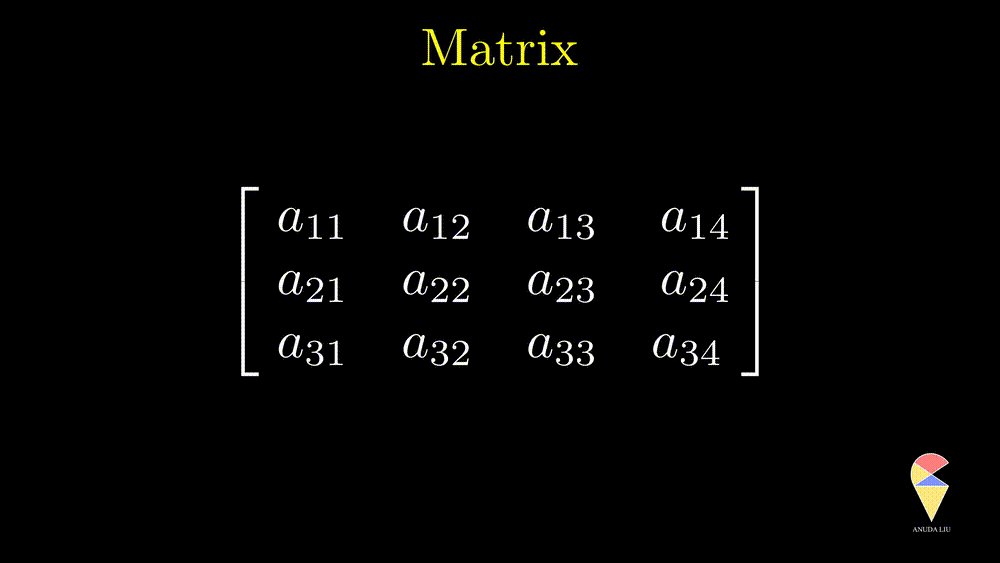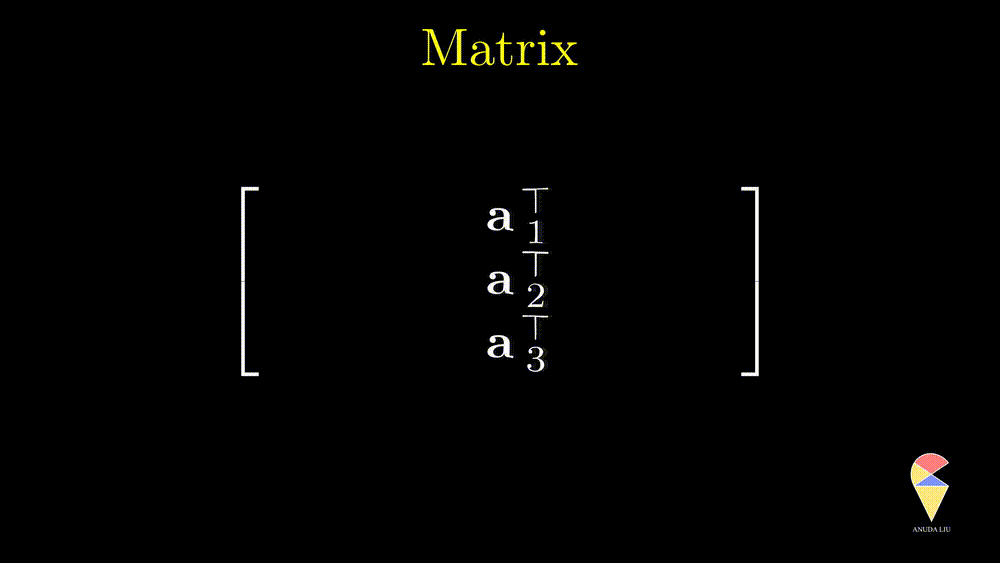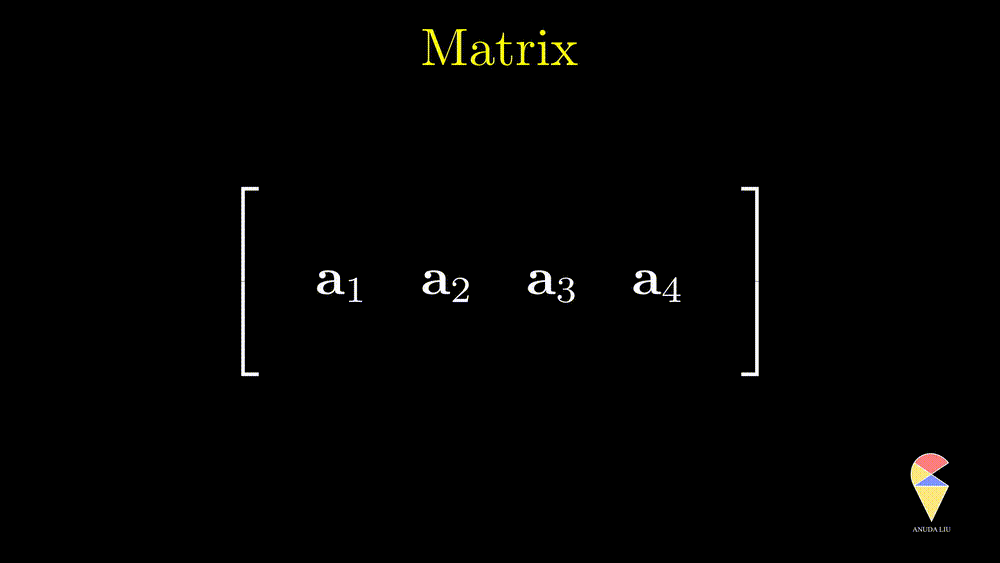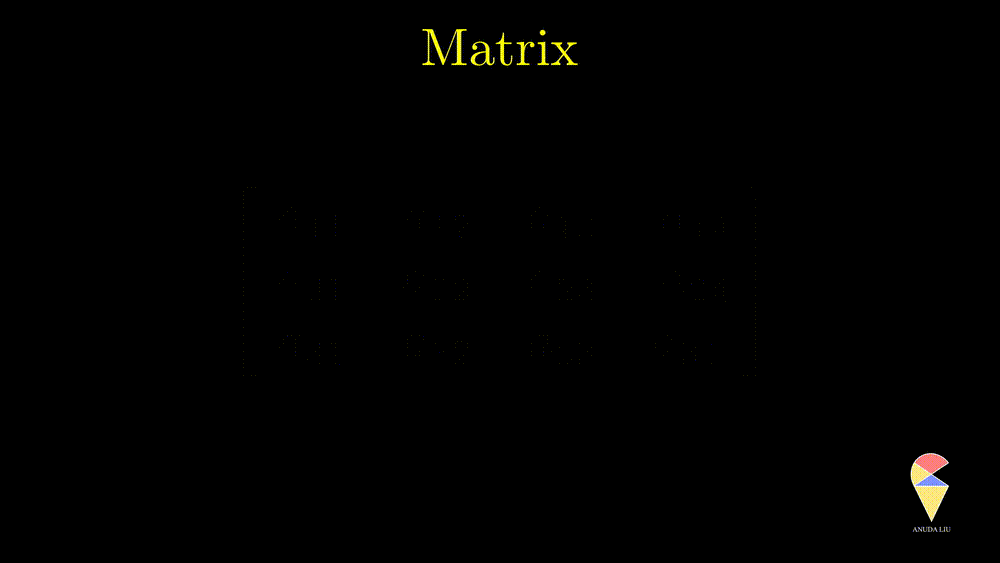
Matrix, true colors
The definition of the matrix above is very straightforward and very helpful when we understand a data matrix in MDA. However, the disadvantage of this definition is that it is too dry, and we cannot understand it from a functional point of view as well as a geometric point of view. Let’s take a look at what its true color. Let’s turn back to the concept of ‘linear combination’ and watch the following animation.
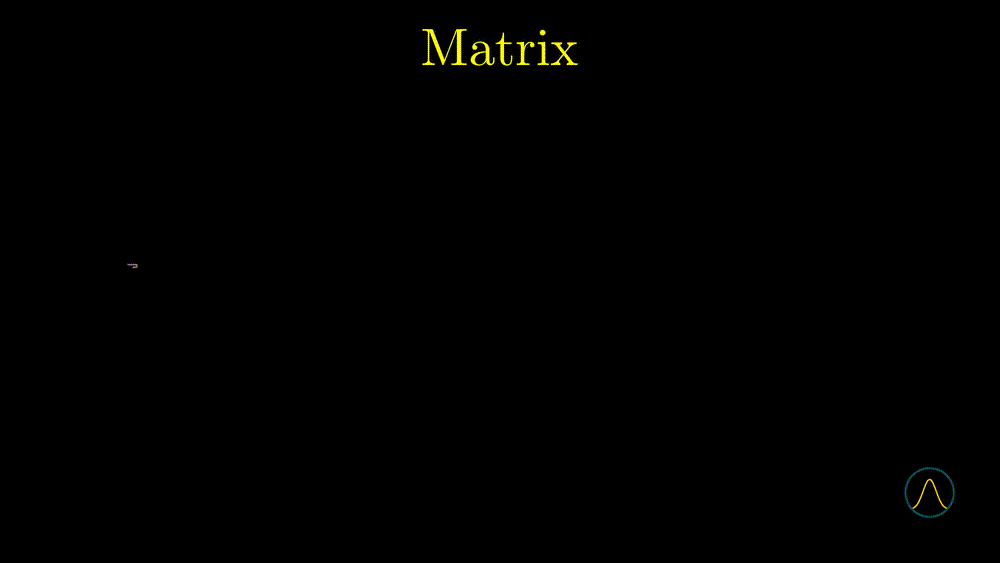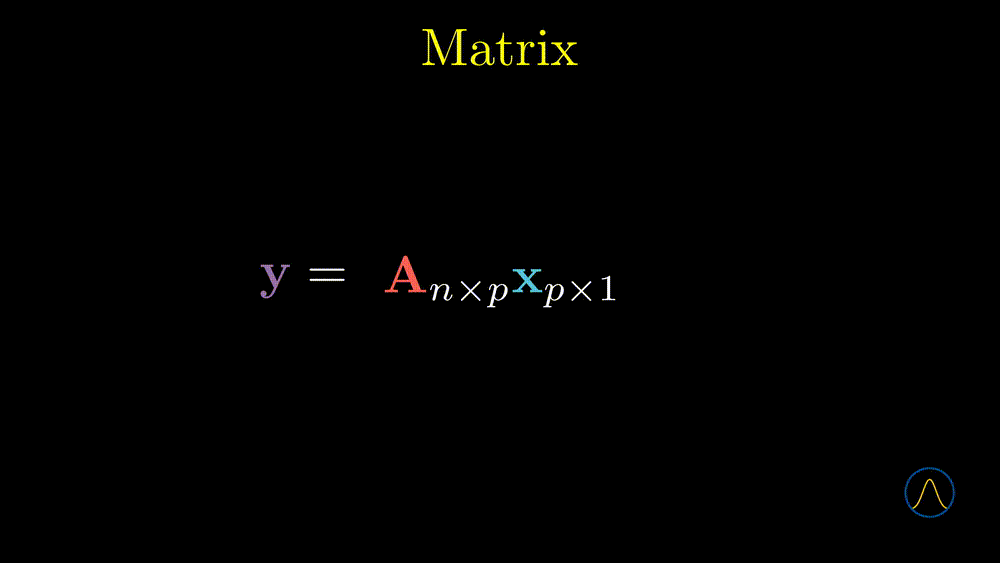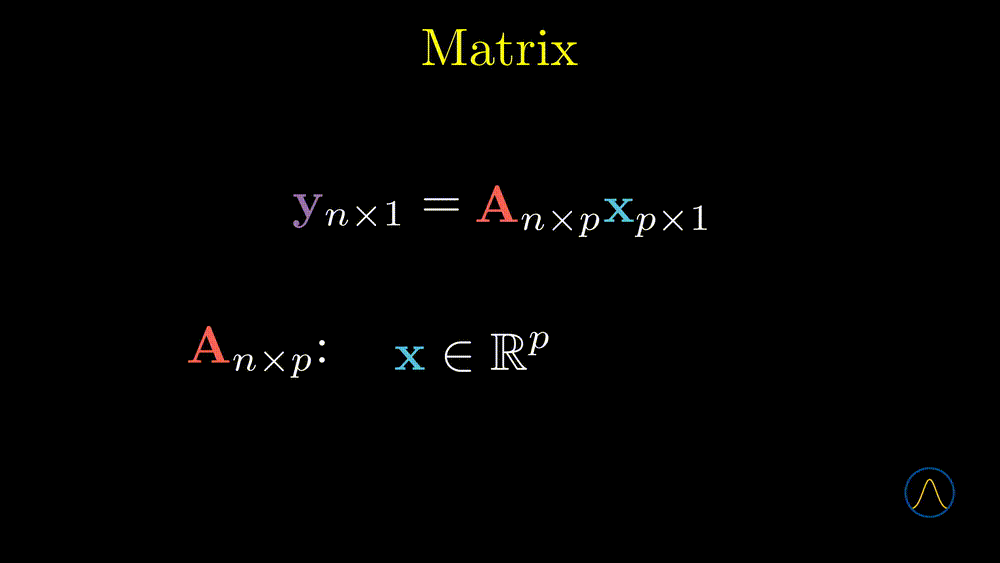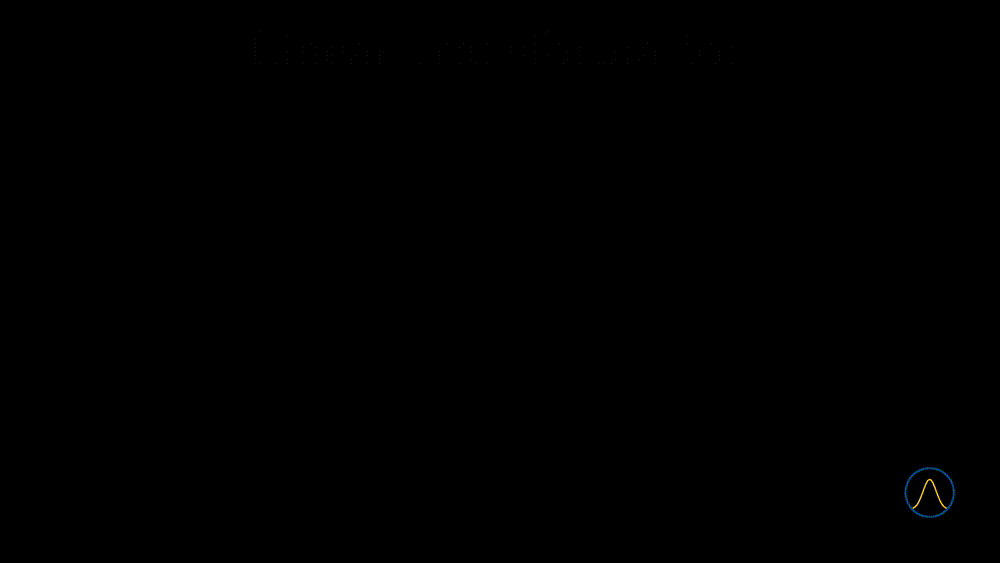
From this animation, we can see that the \(n \times p\) matrix \(\textbf{A}\) determines a map (function) from the \(\mathbb{R}^p\) space to the \(\mathbb{R}^n\) space. We call this map or function a linear transformation. In some sense, the matrix can be viewed as a bridge between two spaces.
Remark: we also want to emphasize that the meaning of an action that pre-multiply a vector by a matrix, \(\textbf{Ax}\), even though we have not defined matrix multiplication yet. Keep in mind that this action means that one uses the elements of \(\textbf{x}\) as coefficients to calculate the linear combination of column vectors of the matrix \(\textbf{A}\). It is very helpful when we discuss the next important concept, the rank of a matrix.
