Proceptron Algorithm
With the discussion above, at least for me, the weights vector of a perceptron classifier is like a sword of judgment, wielded to evaluate all cases. So, I just name proceptron algorithm as finding sword of judgment algorithm. You may remember the brute force idea, so the next question is whether we have a clever way to quickly find the sword of judgment instead of trying all possibilities.

Before we begin to understand how this algorithm works, we must first reach a consensus that no matter how we look for it, we must have a starting point, and this starting point is preferably random. If you agree with me, let’s randomly pick up one initial guess of the sword (weights vector) in the following conceptual example.
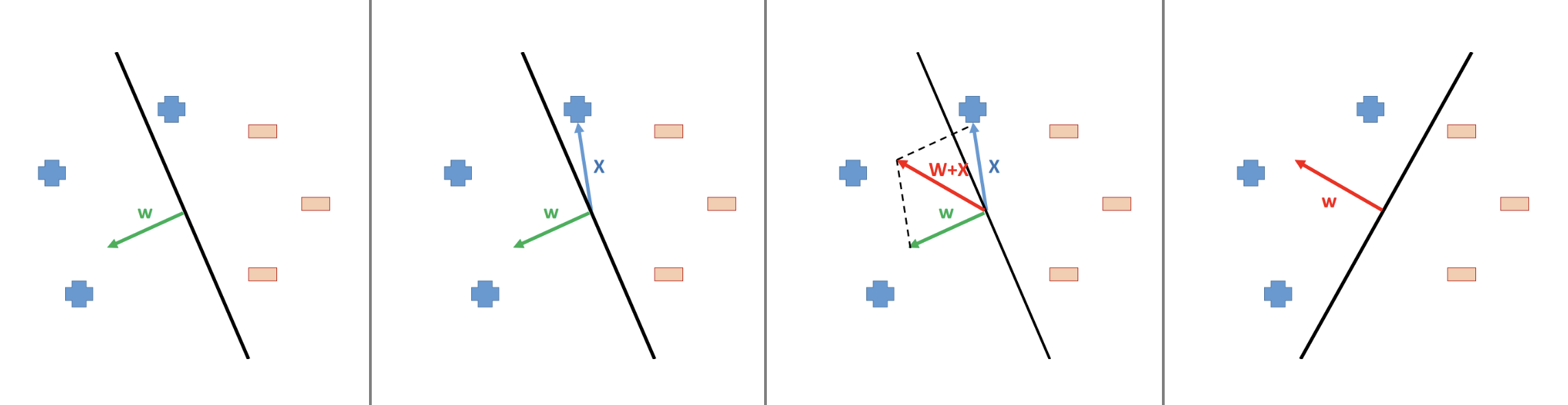
This initial guess is not too bad since it only made one mistake, see the 2nd column of the image. This case is a positive case but wrongly predicted as negative. So, we need to correct this weights vector such that the corresponding decision boundary will be rotated clockwise slightly. From the 3rd column of the image we can see that, this aim can be achieved by updating the weights vector as \[ \textcolor{red}{\textbf{w}}^{\text{new}} = \textcolor{green}{\textbf{w}}^{\text{old}} + \textcolor{blue}{\textbf{x}} \]
By the Parallelogram Law (read about vector addition), the old weights vector will be rotated clockwise, thereafter the decision boundary is corrected properly.
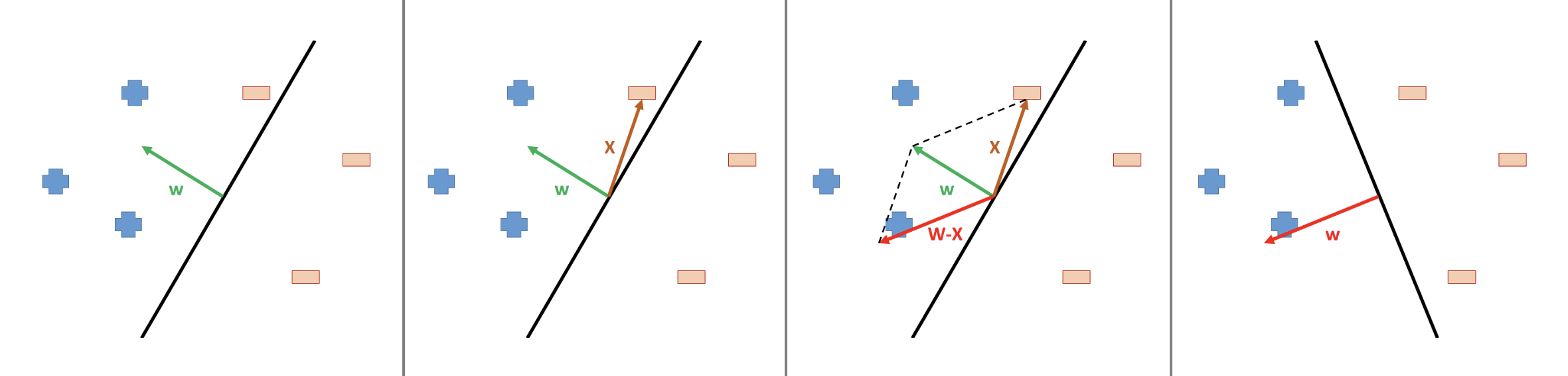
Suppose the mistake by the initial guess of sword (\(\textbf{w}\)) happened for a negative case, see figure below. In this case, we need to update the weights vector as
\[ \textcolor{red}{\textbf{w}}^{\text{new}} = \textcolor{green}{\textbf{w}}^{\text{old}} - \textcolor{red}{\textbf{x}} \]
such that the decision boundary will be anticlockwise slightly.
Notice that the target variable \(y = -1\) or \(+1\), therefore we can integrate the two updating rule as one:
\[ \textcolor{red}{\textbf{w}}^{\text{new}} = \textcolor{green}{\textbf{w}}^{\text{old}} + y \textbf{x} \]
Now, we have actually found a clever way to search for the sword of judgment. Basically, we can do this. First, number all cases, and then randomly pick an initial guess for \(\textbf{w}\). After these are prepared, we start to use this sword to test cases in the order of numbers. If we find a wrong judgment, such as number 3, then we correct this sword according to the updating formula above. After the correction, continue to judge in order, that is, start judging from number 4, and continue to correct the error. Repeat this process, and when we find a real sword that can correctly judge all cases, we stop the search process. This is the so called Proceptron Algorithm:
Proceptron Algorithm:
Inputs: y nx1 vector taking vaules -1 or 1, X nxp matrix
Initialization: weight vector w randomly initialized
While(All cases are correctly classified){
for(i in 1:n){
if(case i is misclassified){
w = w + y[i]X[i, ]
}
}
}Below, you can see an animation presenting the Proceptron Algorithm in action.
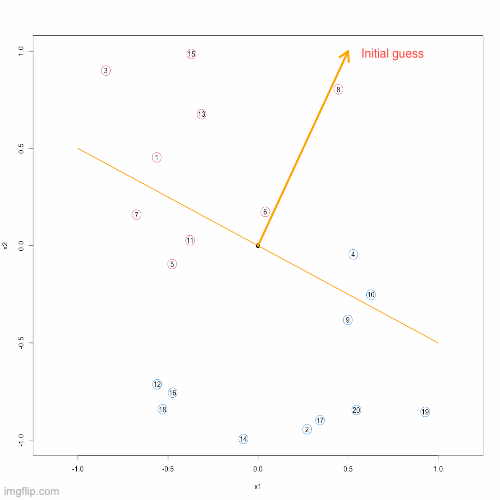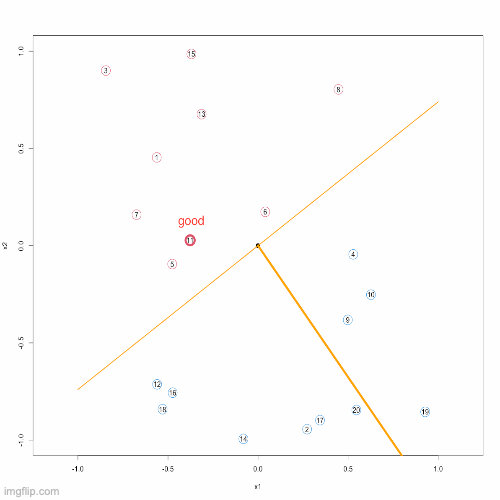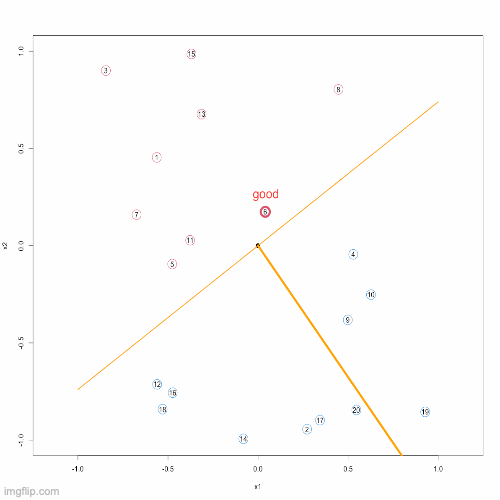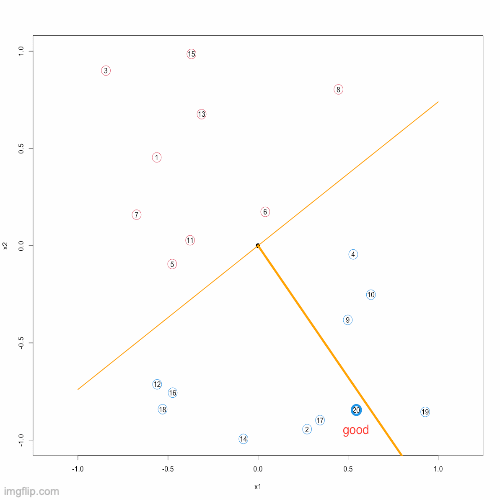
Remarks:
- This algorithm works, that is, as long as we follow this algorithm, no matter where we start, we can always find the sword of judgment.
- However, as you may have realized, this algorithm has a prerequisite, that is, our training samples are linearly separable. In other words, we can find a straight line (2D case) to split the sample space, all positive and negative examples stand on each side, or we will not make any mistakes in the training samples.
- In addition, you may also find that the “reasonable” \(\textbf{w}\) obtained by this algorithm is not unique, that is, there exist many swords of judgment, and which one we finally get depends on our initial guess.
