4. Discussion
Let’s conclude this lecture with a discussion. We call PCA a data-driven solution, meaning it does not rely on any prior information. However, it is important to emphasize that PCA is merely a linear feature extraction method. The concept of linearity is straightforward: all extracted feature variables are just weighted sums of the original variables. But how can we understand linearity from a geometric perspective? Let’s explore this idea with the following toy example.
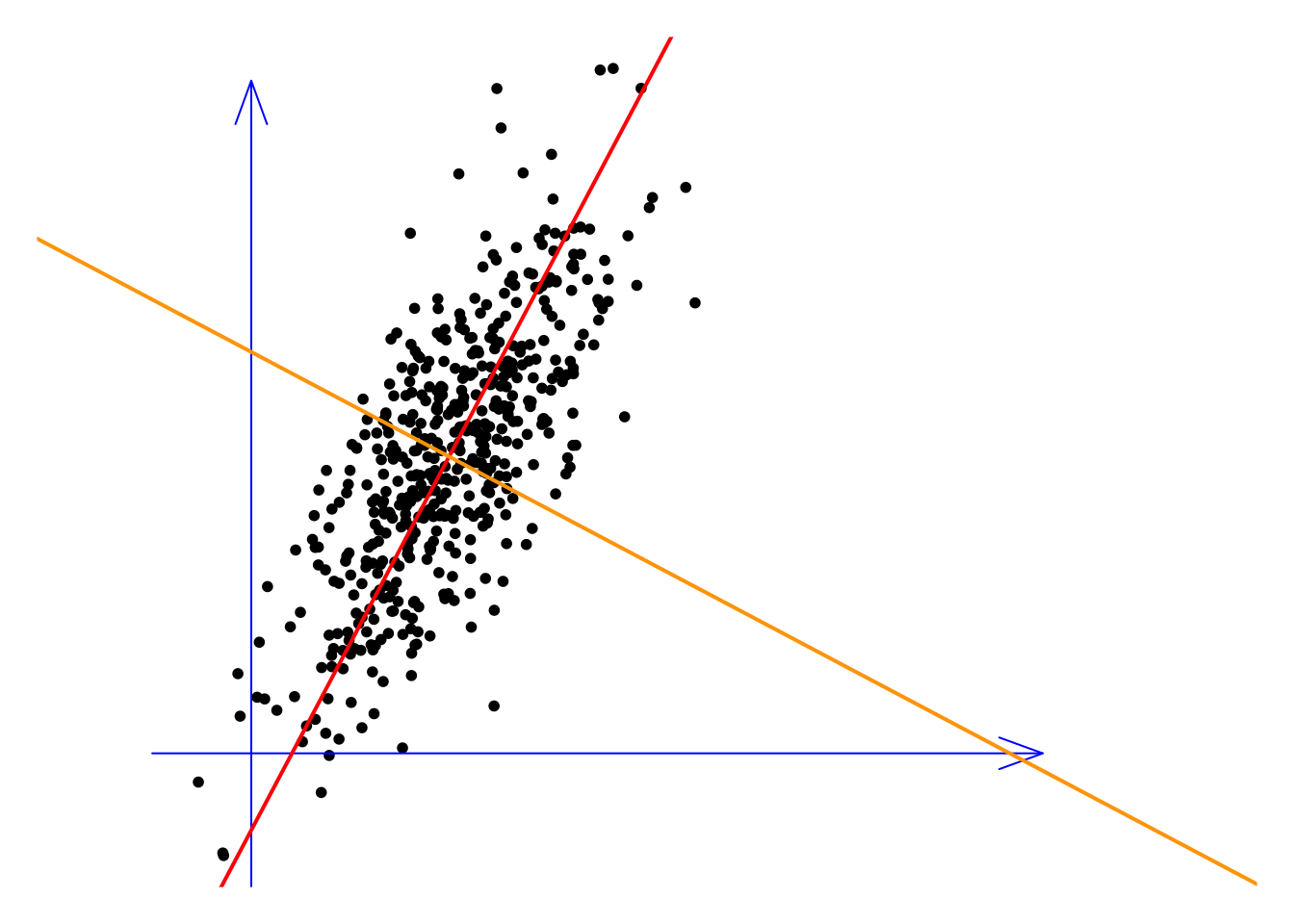
In this example, we have two variables, or two dimensions, represented by the blue coordinate axes. The red and orange lines represent two sets of PC weights, meaning the new variables are the projections of all the observations onto these lines. This requires a bit of imagination. Imagine that all the observations fall perpendicularly onto the red line, which gives us the first new variable. Similarly, by projecting onto the orange direction, we get the second new variable. It’s easy to see that the variance (or information) along the red line is much higher than that along the orange line. Therefore, we can discard the orange variable, effectively reducing the dimensionality while preserving most of the information. Therefore, the linearity of PCA lies in the fact that we are simply re-examining the original feature space from different angles. In other words, we do not disturb the relative positions of the original observations.
The advantage of PCA is that the algorithm is simple and can be easily understood from a geometric perspective, but its limitations are quite apparent as well. First, its feature extraction does not rely on any target information to guide it. The feature extraction process only depends on the covariance structure of the original data. Second, its feature extraction capability is quite limited. We can see that all possible feature extraction methods are determined by the covariance structure inherent in the data. At most, we can have as many feature extraction functions as there are original variables, but most of them will be useless. Therefore, PCA is NOT very flexible, and when the problem becomes complex, it often fails to provide an effective feature extraction solution.


PCA is like God rotating a globe, viewing what happens on this blue planet from different angles. When there’s a problem, God steps in to fix it. However, this gentle approach is linear. But when humanity presents too many complicated challenges, even God might be powerless, allowing the devil to intervene with non-linear methods in extreme ways to solve the problem.
This might not be the best analogy, especially since I’ve received warnings and restrictions while generating images with ChatGPT, but it is indeed quite vivid. So, let’s remember to take care of our beautiful blue planet. 🌍
