3.2 Random Variable and Distribution
Discussing the probability notion for events can often be cumbersome. For example, in the coin example, we have to write texts to represent it. To simplify the expression, we can use a capital letter \(X\) to represent the result of flipping a coin. It has two possible values, \(0\) and \(1\) which indicate getting a Tail and a Head respectively. Then the probability of that event can be represented as \[ \Pr(X = 1) \] This letter \(X\) is so powerful that it encompasses not only the two possible outcomes of one flipping but also represents all potential results each time you flip this coin. We call this letter \(X\) as a random variable which can be understood as a description of the results of a certain experiment. Conventionally, it is usually presented by a uppercase letter and we use lowercase letter, e.g. \(x\), to represent its realization or observation.
Note: the mathematical definition of a random variable goes beyond this and is much more profound; however, this understanding of random variables is sufficient for practical applications.
If the role of a random variable were merely to use a symbol to represent an experimental outcome, it wouldn’t be nearly as compelling. Its essence lies in its distribution. Through the distribution of a random variable, we can abstract the common features of a wide range of random events. For example, consider \(X\) in the context of a coin toss. If we specify that \(X\) takes the value 1 with a fixed probability \(\pi\) and 0 with a probability of \(1 - \pi\), we obtain a random variable with a specific distribution, commonly referred to as a binary distribution or Bernoulli distribution random variable. It can be denoted as \(X \sim \text{Ber}(\pi)\), and its distribution can be simply described as the evaluation of the probability for each possible outcome, i.e.
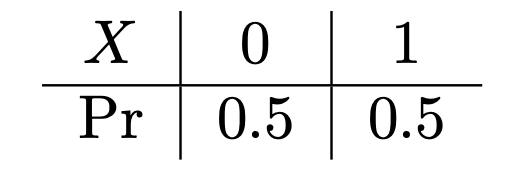
This information of distribution also can be represented by a formula,
\[ \Pr(X = k) = \pi^k(1-\pi)^{1-k} \] where the possible value of \(k\) is 0 and 1, and \(0<\pi<1\). It is called probability mass function (p.m.f).
In this way, the symbol \(X\) becomes much more powerful. The Random variable and its distribution can help us get away from the whole coin-flip thing. The symbol \(X\) is elevated, and it becomes a probabilistic model. It can not only represent the random experiment of flipping a coin but also depict the probability of randomly selecting a man in Umeå city center, or describe the incidence of a certain disease within a specific population over a certain time period in a given region.
Another example: One also can define a random variable \(Y\) denotes the result of throwing a dice, then it has 6 possible values, \(1\) to \(6\). Since the probabilities of getting all possible values are equal, \(1/6\), it is called the discrete uniform distribution. ( PA ) The p.m.f is \[ \Pr(Y = k) = 1/6 \] where \(k = 1,2,\dots,6\). There aren’t necessarily only six possible outcomes; you can increase the number of possible values, allowing this probabilistic model to cover a broader range of random phenomena.
More possibilities, for example, one can use \(Z\) to denote a random variable that presents the number of accidents in a certain time period, for example, the number of traffic accidents in certain area in one month. In this case, the possible values should be \(1,2,3,4,\dots\). From this phenomenon, we can abstract the Poisson distribution which models the number of times an event occurs in a fixed interval of time or space, under the conditions. The p.m.f is leave to you to explore.
Random variable with certain distribution also can help us simplify the calculation of the probability of an event. Let’s see the next example, Binomial distribution, denoted as \(X \sim \text{Bin}(N,p)\). The random variable \(X\) presents the number of positive results among \(N\) independent binary results experiment. The probability that getting a positive result in one experiment is \(p\). Obviously, the possible values of \(X\) are integers from \(0\) to \(N\), and the distribution can be represented as \[ \Pr(X = k) = \frac{N!}{k!(N-k)!} p^{k}(1-p)^{N-k} \] where the exclamation sign denotes factorial, i.e. \(N!=N(N-1)(N-2)\dots1\). It is easy to see the probability of the relatively complicated random event discussed before, you get \(2\) heads after flipping a coin \(6\) times, which can be calculated by this distribution. We can define a random variables the number of getting heads after flipping a coin \(6\) times, so \(X \sim \text{Bin}(6,0.5)\). Replacing \(N=6\), \(p=0.5\), and \(k=2\) in the formula above, one can easily verify \(\Pr(X=2) = 0.234375\).
