# randomly generate 5000 numbers taking values 0 or 1 and save in x
set.seed(8312)
x = rbinom(1000,1,0.5)
# calculate the cumulated ratio
ratio = cumsum(x)/(1:1000)
plot(ratio, type = "l")
abline(h = 0.5, col = "red")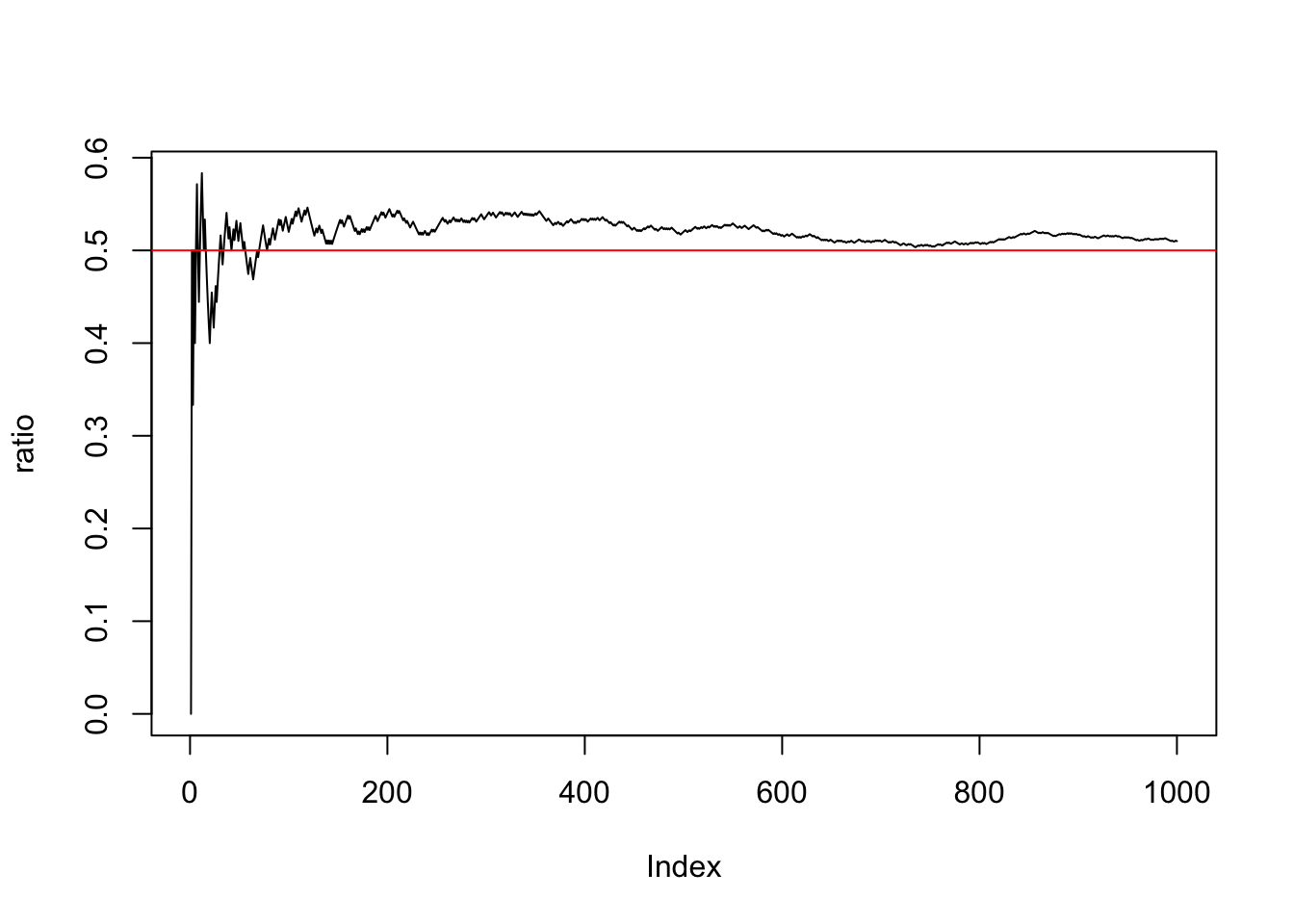
3.1 From Frequence to Probability
Early on people realized that there are many things in the real world where the outcome is uncertain, such as one doesn’t always get a head when flipping a coin, or doesn’t always get a certain number when throwing a dice, and so they refer to this kind of event as random event. At the same time, mathematicians also had found that the percentage of getting heads always seems to be close to \(0.5\) when they repeatedly flip an even coin. The following r codes simulate this process:
0.5, that is 1/2, has different meanings for its numerator and denominator; the denominator is the number of all possible outcomes (Head or Tail), while the numerator is the number of outcomes included in this event. Thus, mathematicians defined the first probability model in which the possibility of a random event occurring can be quantified by the ratio of the number of outcomes associated with the event to the number of all possible ones. Meantime, we refer to this measure of possibility as the probability of an event.
\[
\Pr \left( \text{Event} \right) = \frac{\text{number of outcomes associated with the event}}{\text{total number of all possible outcomes}}
\] In the coin example, all possible outcomes are \(H\) and \(T\), and the outcome associated with the event, getting a head, is \(H\). So, the probability that get a head when flip a coin is \[
\Pr(\text{Get a head when flip a coin}) = \frac{1}{2}
\] Since the number of outcomes associated with the event is always less than the total number of all possible outcomes, the probability defined by this model is always a number between 0 and 1, which fits our intuitions.
Based on this model, one can easily quantify the possibility of an event if one gets the number 3 when throwing a dice as \(1/6\). Before providing more examples, I have to emphasize that probability is a mathematical concept that only exists in our rational world. That is, you can only get a number which is 3 or not 3 after throwing a dice. Also, even if you throw a die over and over again for the rest of your life, the number of times you get a 3 as a percentage of your total throws will only be very close to \(1/6\).
( NE ) Let’s explore some more complex examples. First, what is the probability that you get a number less than 5 by throwing a dice? Using the model above, the total number of outcomes of throwing a dice is 6 and there are 4 potential outcomes all satisfy this condition, therefore this probability is \(2/3\). Second, what is the probability that you get 2 heads after flipping a coin 6 times? Again, the total number of possible outcomes is \(2^6\) and the number of outcomes satisfying this condition is \(15\), therefore the probability of this event is \(0.234375\). Obviously, the second example is harder than all the examples before, and you probably need some knowledge of permutations and combinations to understand the meaning of numbers \(2^6\) and \(15\). However, this is not the main purpose here. Also, calculating such numbers is not essential to understanding the probability model. Of course, if you’re interested in these types of questions, consider solving some problems from a book on probability theory, which is a good mental exercise. For example, you might think carefully about why a full house can beat a flush in Poker? (ToDo4Sia: Write a note discussing how you teach your son about permutations and combinations.)
